.NET System.Random の実装と欠陥について ~ 重箱の隅をつつきたおす ~
はじめに
.NET (C#) には、組み込みの擬似乱数生成器 System.Random が用意されています。
ここでは、 System.Random の実装と性質・ひいては欠陥について、可能な限り深くまで調べて難癖をつけていきます。
結構いろいろあって内容が増えてしまったので、雰囲気をつかみたい方は目次をみてください。
- はじめに
- 内部実装
- 外部実装・その他の問題
- おわりに
内部実装
ここでは、 System.Random に実装されているメソッドの中身を詳しく見ていきます。
内部実装の参照
System.Random の内部実装は以下サイトで確認することができます。
両者は基本的には同一ですが、 new Random() の動作だけ異なります。詳細については new Random() の項を参照してください。
System.Random の定義だけ並べると以下のようになっています。ひとつひとつ追っていきたいと思います。
public class Random { public Random(); public Random(int Seed); public virtual int Next(); public virtual int Next(int maxValue); public virtual int Next(int minValue, int maxValue); public virtual void NextBytes(byte[] buffer); public virtual void NextBytes(Span<byte> buffer); // .NET Standard 2.1~ public virtual double NextDouble(); }
new Random()
ライブラリ側で int 型のシード値を選択し、後述する new Random(int Seed) を呼び出します。
このコンストラクタだけは、.NET Framework と .NET Core 以降で動作が異なります。
.NET Framework: 同タイミングでの初期化でシードが重複する問題
.NET Framework では、 Environment.TickCount (システム起動後のミリ秒単位の経過時間) をシードに用います。
そのため、同じタイミングで生成された Random はかなり高い確率で同じ乱数列を返すようになってしまいます。
例えば、同一フレーム中に別々の場所でインスタンス生成した場合などで、意図せず出力が重複する事故が予想されます。
余談ですが、手元の C# Interactive で試してみたところ、1 ミリ秒の間に 2 万個程度の同じ系列を返すインスタンスを生成できました。
.NET Core: シード重複問題の改善
対して .NET Core 以降では、このような問題が起こらないよう対策がとられています。
具体的には、スレッドごとに独立な static Random インスタンスの Next() をシードとします。そして、シードを生成するほうは普通の static な Random インスタンスの Next() をシードとしています。そしてそして、そのシードを生成するほうは、extern 関数 SystemNative_GetNonCryptographicallySecureRandomBytes をシードとしています。
要するに、外部取得シード → static Random → ThreadStatic Random → インスタンス Random 、という流れで初期化されていきます。
なお、 SystemNative_GetNonCryptographicallySecureRandomBytes の Unix 環境における実装 は、
- Arc4Random が利用できればそれを、
- できなければ、
/dev/urandom/とlrand48()を xor したものを
返すようです。
ところで、 Next() の性質上、シードに int.MaxValue は絶対に選択されなくなりました。 (.NET Framework では起動から 25 日弱経てば生成される可能性がありました。) 詳細は Next() の項で述べます。
余談: 同じアルゴリズムによる初期化について
乱数のシード設定に同じ擬似乱数生成アルゴリズムを用いるのは果たして大丈夫なのか、という懸念が少しだけあります。シード設定には根本的に構造が異なる擬似乱数生成器を用いるほうがよい、気がするので… xoshiro/xoroshiro の作者のサイト にはこのような記述があります。
as research has shown that initialization must be performed with a generator radically different in nature from the one initialized to avoid correlation on similar seeds.
(肝心の "research" の中身にアクセスできないので厳しいですが、 Mersenne Twister の作者が書かれているようです)
new Random(int Seed)
Seed をもとに内部状態を初期化します。同じ Seed を指定すれば、完全に同じ出力列が得られます。
初期化に使われているアルゴリズムは、微妙に根拠が怪しい気もするラグ可変の Fibonacci 法らしきものと、遷移関数と異なるラグを持つ Lagged Fibonacci 法 4 周分です。 (もし根拠をご存知の方がいらっしゃれば教えていただけるとありがたいです。)
なるべく分かりやすいように整理した等価なコードを示します。
// 内部状態: int[] _seedArray = new int[56]; // [0] は未使用 int _inext; // I(ndex) Next ? int _inextp; // I(ndex) Next P ? // Seed の絶対値を取る Seed = (Seed == int.MinValue) ? int.MaxValue : Math.Abs(Seed); // 定数 161803398 は黄金比が由来とのこと _seedArray[55] = 161803398 - Seed; // ラグ可変の Fibonacci 法らしきもの (?) { int prevState = _seedArray[55]; int nextState = 1; for (int i = 1; i < 55; i++) { int leapIndex = 21 * i % 55; _seedArray[leapIndex] = nextState; // (prevState - nextState) mod int.MaxValue のイメージ nextState = prevState - nextState; if (nextState < 0) nextState += int.MaxValue; prevState = _seedArray[leapIndex]; } } // ラグの異なる Lagged Fibonacci 法で 4 周する for (int k = 0; k < 4; k++) { // lagIndex は (1 + (index + 30) % 55) に等しい for (int index = 1, lagIndex = 32; index < 56; index++, lagIndex++) { // ([index] - [lagIndex]) mod int.MaxValue のイメージ _seedArray[index] -= _seedArray[lagIndex]; if (_seedArray[index] < 0) _seedArray[index] += int.MaxValue; if (lagIndex == 55) lagIndex = 0; } } // ラグ (インデックス) の初期化 _inext = 0; _inextp = 21; // 💀💀💀
なお、初期化後の _seedArray の各要素は の範囲になります。
int.MaxValue は含まない非負の値をとるのが重要なポイントです。
絶対値が同じ Seed は同じ乱数列を生成する
Seed は絶対値をとってから計算するため、例えば new Random(401) と new Random(-401) は同じ乱数列を生成します。
なお、Seed == int.MinValue の場合はなぜか int.MaxValue として扱われます。したがって、全ての int 値の入力 ( パターン) に対して、実質のシード値は
0:0の 1 個1 <= x < int.MaxValue:x, -xの 2 個int.MaxValue:int.MaxValue, -int.MaxValue, int.MinValueの 3 個
と微妙に偏ります (?) 。
初期状態のパターン数が少ない
以上から、初期状態は パターンに限定されます。内部状態のとりうるパターン数
*1 よりかなり小さく、ブルートフォースでもなんとかなる程度の量です。
内部状態 _seedArray の無駄
_seedArray は要素が 56 個あるにもかかわらず、実際に使っているのは [1] ~ [55] までで [0] は使用されておらず、残念感があります。55 個しか使わないのが理論上正しいので、 0 基点にして 55 要素で良かったのでは、と思ってしまいます。
余談: 初期化時の制約について
System.Random では上記のアルゴリズムで初期化が行われていますが、別のアルゴリズムで差し替えようと思ったとき (?) 、問題なく初期化するにはどうすればよいでしょうか。
擬似乱数生成器の設計によりますが、一般に内部状態を初期化する際は特殊な条件を満たす必要があります。例えば Xorshift では全 0 以外で初期化する必要があり、そうでないと永遠に 0 を吐き出し続けてしまいます。
System.Random では、内部状態にひとつでも非 0 の要素があれば (全 0 でなければ) 大丈夫です。ただしこれは法 上で正しく設計されていた場合の話です。正しく、がどういう意味かは
Next() の項で説明しています。
もし法 ならば、ひとつでも奇数の要素があれば大丈夫です。 (つまり、どれかは最下位ビットが 1 になっている必要があります。) 少しだけ条件が厳しくなります。
ただし、これらは最低条件 (最長周期を満たす条件) であって、まともな初動の出力が得られるかはまた別の話です。例えば {1, 0, 0, 0, ..., 0} といった極端な初期状態を設定すれば、しばらくの間 0 とか 1 のようなものが出力され続けるでしょう。現実には、なるべくランダムなバイト列で埋めてから、これらの条件を満たすかどうかチェックする (ダメならやり直す) 、という流れになります。
ただ、 System.Random ではその手のチェックは入っていません。要素が 55 個もあるのでどれかは条件を満たすだろう、という楽観的な見込みなのかもしれません (実際問題ないとは思いますが) 。
また _inext や _inextp といったインデックスについては、別種の注意を払って初期化する必要があります。コメントの意味深な 💀💀💀 については、次の Next() の項で解説します。
int Next()
0 <= x < int.MaxValue の範囲の擬似乱数を出力します。
Next() は他の出力系メソッドのベースになっています。他のメソッドは、このメソッドの出力を加工して出力しています。
(実際のコード上では InternalSample() というメソッドに実装されていますが、Next() と完全に等価なので、簡単のためこのように表現します。)
Next() 、つまり System.Random の遷移関数は、 MSDN にもあるように Lagged Fibonacci 法の一種である「引き算法」で実装されています。
The current implementation of the Random class is based on a modified version of Donald E. Knuth's subtractive random number generator algorithm.
ちなみに、文献としては TAOCP が参照されていますが、実際のコードは Numerical Recipes の ran3 が原典のようです。
引き算法の遷移関数を漸化式で書くと以下のようになり、名前通り引き算で遷移していることが分かります。
なお、ここでの は剰余演算子
% とは微妙に異なり、必ず非負の値をとるものとします。 例えば、 です。
System.Random においては、 です。
Next() を分かりやすいように整理した等価なコードを示します。
// index を +1 して、配列範囲からあふれたらループさせる (% 55 (+1) のイメージ) if (++_inext >= 56) _inext = 1; if (++_inextp >= 56) _inextp = 1; // ([_inext] - [_inextp]) mod int.MaxValue のイメージ _seedArray[_inext] = _seedArray[_inext] - _seedArray[_inextp]; if (_seedArray[_inext] < 0) _seedArray[_inext] += int.MaxValue; return _seedArray[_inext];
さて、擬似乱数の紹介と言えば「周期」が代表的ですが、System.Random の周期は不明です。正しく実装された場合よりも短くなっていると推測されます。
なぜかというと、誠に遺憾ながら System.Random の遷移関数の実装に重大な誤りが複数含まれているためです。
遷移関数の実装ミス (1) - ラグ k の指定
誤りのひとつは、 Random(int seed) コンストラクタの項で意味深な 💀💀💀 を貼っていた _inextp = 21; で、正しくは 31 を代入すべきでした。この値は 2 つめのラグ (漸化式での ) を指定するものです。
Lagged Fibonacci 法で最大周期を達成するためには、法 の場合はラグ
に
上の原始多項式の指数を用いる必要があります。 (とても雑に言えば、
は適当に決めてはダメで、特別な場合だけ最大周期になるということです。) 例えば、以下に示す
は
上での原始多項式です:
この指数である 55 と 24 をラグとして用いることで、最大周期を達成できます。 _inextp の正しい初期値 31 は、 55 - 24 から来ています。
そして、System.Random で使われているラグ を多項式で表した
は、原始多項式にはなりません (既約多項式ですらありません。詳細は後述) 。
そのため、
System.Random の周期は、達成可能な最大周期よりも短くなっており、かつシードによって周期長が変動してしまう可能性があります。
余談ですが、皮肉にも new Random(int Seed) における 2 つめの初期化フローにおいては、 _inextp = 31; 相当の "正しい" 実装になっています。
遷移関数の実装ミス (2) - 法 m の指定
また、 コピペ元 実装のベースになったと思われる Numerical Recipes の ran3 の実装と比べると、 の値も
から
に変更されています。さらに言えば、原典となる TAOCP の
ran_array では でした。MSDN の modified version という記述はこの
の変更を指しているものと思われます。 *2
法 の場合は、下位
番目のビット (最下位は 0 とします) の周期が
となるため、最大周期は
となります。 *3
System.Random でいえば です。
しかし、 System.Random においては で、これは奇数 (もっと言えば素数) なので、以上の議論は適用できません。
私が調べた限りでは、少なくとも「
上の」多項式
が原始多項式である必要がありそうです。しかし、 (そもそもラグが誤っているのを無視しても)
上で原始多項式であることと
上で原始多項式であることは全く関係がないのと、
上での原始性判定は法の大きさのために困難であると推測されるのとがあります。原始性判定には
の素因数分解を知っている必要がありますが、巨大なため FactorDB でも完全な分解が載っておらず (297 桁の未分解の数を含みます) 、まだ人類は知らない可能性が高いです。
ちなみに の場合は、理論上の最長周期は
になります。
余談: m = 2 ^ 31 の場合の最下位ビットの周期について
注記: この項での内容は実際の
System.Randomには適用できません。参考情報程度にお考え下さい。
オリジナルの の場合は解析が厳しいことを上で述べましたが、 +1 して
とした場合なら、法が 2 のべき乗になるので本来の
上での理論が適用可能であり、話が比較的簡単になります。
System.Random の 上での多項式は、 Wolfram Alpha 先生曰く以下のように因数分解されます:
なお、 は原始多項式となることを確認しています。
ここで、内部状態の最下位ビットだけを考えることにすると、遷移式 の減算を
のように XOR に置き換えても意味は変わりません (参考) 。
XOR に置き換えた式から、最下位ビットは LFSR (Xorshift や Mersenne Twister の仲間) と同じ働きをすることが分かります。
LFSR では、 回の遷移を
と多項式で表すことができます。ここで、
にすると
にかかわらず = 何度遷移しても 0 になるので、周期が 1 になってしまいます。 (そのため、LFSR ベースの擬似乱数生成器では「全 0 以外で初期化せよ」とよく書かれています。)
今回は法とする多項式が原始ではないので、計算が少しだけ複雑になります。
を因数分解した
について、
を満たす
の位数 (
を満たす最小の自然数
) の最小公倍数が、初期値
から始まる系列の周期となります。 (
は
上の原始多項式なので、位数はそれぞれ
となります。) 逆に考えると、
となる
が存在すれば、その分だけ周期が短くなる、ということです。
以上から、全てのとりうる初期状態 パターン内での、最下位ビットの周期の内訳を計算したものを下表に示します。
最初の 3 列が
が 0 かそれ以外かを示します。「ストリームの本数」は初期値の個数を周期で割ったもので、互いに交わらない乱数列の数を示します。 (ストリーム A で出現する数値は他のストリームでは一切出現せず、その逆も同様です。初期値を変更しない限りストリームが変わることはありません。)
なお、最初の 0, 0, 0 の列は
0 で初期化した場合で、一応含めましたが実質ノーカンです。
| f1 | f2 | f3 | 属する初期値の個数 | 周期 | ストリームの本数 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | any | 134217727 | 134217727 | 1 |
| 0 | any | 0 | 524287 | 524287 | 1 |
| 0 | any | any | 70368609435649 | 70368609435649 | 1 |
| any | 0 | 0 | 511 | 511 | 1 |
| any | 0 | any | 68585258497 | 134217727 | 511 |
| any | any | 0 | 267910657 | 267910657 | 1 |
| any | any | any | 35958359421616639 | 70368609435649 | 511 |
割合にすると 99.9998 % ぐらいは周期 になりますが、それでも実現可能な最大周期
よりかなり小さくなります。また、とても運が悪いとたった 511 回でループする出力列が割り当てられる可能性があります。
具体例を挙げてみます。最下位ビットだけを集めて構成した MinimalBottomSystemRandom において、初期状態 0x6c98d1cf は表の 2 行目に分類されます。そのため、内部状態は 55 ビット分あるにもかかわらず周期として 134217727 が出力されます。
class MinimalBottomSystemRandom { // State の最下位ビット (0x1) が x[0] の最下位ビット, 次のビット (0x2) が x[1] の最下位ビット, ... を表します public ulong State { get; private set; } const ulong Polynomial = 1 ^ (1ul << 34) ^ (1ul << 55); public MinimalBottomSystemRandom(ulong state) => State = state; public ulong Next() { // 55 bit LFSR として構成します State <<= 1; if ((State & (1ul << 55)) != 0) State ^= Polynomial; return State; } } static void Test() { ulong initialState = 0x6c98d1cf; var rng = new MinimalBottomSystemRandom(initialState); { ulong i = 0; do { rng.Next(); i++; } while (rng.State != initialState); Console.WriteLine($"loops at {i}"); // `loops at 134217727` } }
ちなみに、初期値 0x192b762df1 は 3 行目に分類され、周期 524287 となります。
本項の内容は、文献 *4 を参考にしました。
ただし、記載している値に誤りがあるような気がします。Fig. 30 の累乗の計算に誤りがあったり、 System.Random の多項式の係数を (55, 21) としていたりします。
遷移関数の性質の要約 - 周期は不明
要約すると、 System.Random には周期を保証できる要素が存在しないという、とても悲しい状態にあります。
しかし、これらを修正すると生成する乱数列が変わってしまうため、シードを固定して同じ動作を再現することを期待しているプログラムを壊してしまいます。標準ライブラリのつらさを感じます。
一応 .NET (Framework) のメジャーバージョンをまたいだ場合には、乱数列の再現性は保証しない と明記はされているので、変更することは理論上は可能だとは思いますが、 .NET 5 でも変わらなかったところを見ると…という感じです。
この項は dotnet/runtime に立てられた Issue をもとにしています。別の問題についての言及もあるので、リンクをたどってみると面白いです。
Next() は int.MaxValue を含まない
以上では、 Next() の遷移関数としての性質について述べました。ここからは、出力関数としての特性を観察します。
MSDN にもあるように、このメソッドは 0 <= x < int.MaxValue (== 2147483647) の範囲の乱数を返します。
A 32-bit signed integer that is greater than or equal to 0 and less than MaxValue.
int.MaxValue は範囲に含まれない のが重要なポイントです。
(この制限は、内部状態が同様に 0 <= x < int.MaxValue の範囲を取っており、それをそのまま出力しているためです。遷移関数の説明での によります。)
大変面倒なことに、すべてのベースとなるメソッドの値域が 32 bit 全域を埋めないどころかそもそも 2 のべき乗ではありません。そのため、ビット演算・構造を活用した効率化ができないことが問題になります。例えば、4 バイトのランダムな byte[] を得るために BitConverter.GetBytes(random.Next()) などと書いてしまった場合、[3] の最上位ビットが常に 0 だったり、[0] の確率が偏ったりします。
Next() の出力パターン数は奇素数である - 範囲加工における偏り
また、出力されうるパターンの数 は素数です。
したがって、
以外のすべての x に対して
2147483647 % x > 0 を満たします。
これが何を意味するかというと、出力をある範囲に加工する際、乗算や剰余を使って安直に変換すると必ず余りが出る = 確率に偏りが生まれることを示します。
例えば、 random.Next() % 401 によって 0 から 400 までの値を得たいとします。 *5
この時、 2147483647 % 401 == 327, 2147483647 / 401 == 5355320 となります。したがって、0 ~ 326 までの範囲は 5355321 / 2147483647 、327 ~ 400 までの範囲は 5355320 / 2147483647 の確率で得られます。このように微々たる差ではありますが、確実に差が生まれます。
最も相対的な差が大きくなるのは の場合で、多いほうと少ないほうで 2 倍確率が異なる (
2 / 2147483647 と 1 / 2147483647) ことになります。
一番影響がありそうな事例としては、 random.Next() & 0xff といったコードでしょうか。 の生成器なら偏りなく各ビットを得ることができますが、そうではないので
0xff が 8388607 / 2147483647 、それ以外が 8388608 / 2147483647 の確率で出現します。
最も、偏りについては「変換手法を工夫すれば」回避可能です。ただ、そんな工夫は System.Random には存在せず、むしろ上述した剰余を使う手法よりも偏りが発生する手法を採用しています。これについては Next(int maxValue) の項で説明します。
_inextp は必要か
既に述べた _seedArray の無駄に近い話ですが、これが使用されているのは Next() のほうなのでこちらに書きます。
_inextp は常に (_inext + 20 % 55) + 1 となるので削除可能ではあります。
ただ、都度剰余などの計算をしなくてもよくなるので、一概に無駄とは言えないかもしれません。
実際に確かめてみましょう。変更前後で BenchmarkDotNet を使ってベンチマークを取ってみたところ、速度は全くと言っていいレベルで変わりませんでした (変更前 11.72 ± 0.560 ns 、変更後 11.65 ± 0.303 ns 。± は標準偏差) 。 int 1 つ分とはいえメモリを占有することを考えると、やっぱり不要かもしれません。
// 変更後バージョン。 Next() の先頭だけ抜粋: if (++_inext >= 56) _inext = 1; int _inextp = _inext + 21; // note: ローカル変数なので保存不要 if (_inextp >= 56) _inextp -= 55;
余談: 下位ビットの品質について
線形合同法ベースの擬似乱数生成器では「下位ビットは品質が良くない (周期が短い) のでなるべく上位ビットを使え」「範囲に変換するときに剰余 % maxValue を使うな」とよく言われますが、 System.Random ではどうでしょうか。
ふわっとした説明しかできないので申し訳ないのですが、 System.Random においては問題なさそうです (その他もろもろの問題は見なかったことにするなら…) 。というのも、法が ではないので、最上位ビットの情報が剰余を通じて最下位ビットに伝播するため、すべてのビットの周期が最上位ビットと同様になります。
対して の場合は、ビット間の情報はキャリー (繰り上がり・下がり) のみによって伝播するため下位ビットから上位ビットへの一方通行になります。その場合は前述したように最下位から
ビット目の周期は
となって下位ほど周期が短くなるので、上位ビットを使ったほうが良いことになります。
このように、この問題は線形合同法固有の話ではありません。逆に、線形合同法でも法を奇素数などに設定すればすべてのビットの周期が同じになります。最も、その場合は System.Random と同じようにバイト・ワード全域への均等な出力 (例えば Next() & 0xff) が困難になるので一長一短です。
余談ですが、Xorshift や Mersenne Twister などの LFSR ベースの擬似乱数生成器ではこの問題は生じません。 ビットの状態を持つとき、すべてのビットの周期が
になります。
int Next(int maxValue)
0 <= x < maxValue を満たすランダムな x を返します。
実は Next(0) は有効で、 Next(1) と同様に常に 0 を返します。 Next(-1) ではきちんと ArgumentOutOfRangeException がスローされます。
変換関数は、一旦 0.0 <= x < 1.0 の double 値に変換してから maxValue を掛ける、という手法で実装されています。
等価な実装を示します:
return (int)(Next() * (1.0 / int.MaxValue) * maxValue);
浮動小数点数の丸めによって確率が偏る
double 上で計算しているので、浮動小数点数の丸めによる計算誤差が生じ、結果として確率が偏る場合があります。
Next(int.MaxValue) の場合が分かりやすいので、例に挙げて説明します。出力範囲としては Next() と同じ 0 <= x < int.MaxValue になりますが、Next() と Next(int.MaxValue) の結果は同一の入力に対して等価になりません。 Next(int.MaxValue) は均等な出力を生成せず、絶対に出力されない値とより多く出力される値が存在します。
この問題は、 Next() * (1.0 / int.MaxValue) * maxValue (double 値) の小数点以下のビットがすべて 1 になっていた場合に発生します。具体例を挙げると、Next() == 4194305 の場合の計算結果は内部表現 0x415000003fffffff (10進 4194304.9999999991) をとり、これを丸めた結果 4194304 と元々の Next() と違う値が返ります。
なお、 Next() が前後の数値 4194304, 4194306 を返した場合の計算結果は Next() と同じになります。つまり、Next(int.MaxValue) から 4194305 を得る確率は 0 となり、対して 4194304 を得る確率は 2 / 2147483647 と通常の 2 倍になります。
Next(int.MaxValue) において、入力 ( Next() ) と出力が異なる要素は 9437184 個存在し、全体の約 0.44 % にのぼります。また、出力が異なった結果重複して振り分けられる数も存在することから、絶対出力されない要素が 9437184 個、通常の 2 倍の確率で出力される要素も 9437184 個存在することになります。
このことは目に見える問題となって現れます。 より詳細な解析を行っている文献 によれば、 Next(int.MaxValue) の返り値が奇数となる確率は約 50.34 % (厳密には 1081081855 / 2147483647) となり、明らかに想定される確率 (50 %) から離れています。
int Next(int minValue, int maxValue)
minValue <= x < maxValue の範囲の擬似乱数を出力します。
こちらも、 minValue == maxValue を許容して常に minValue を返します。もちろん minValue > maxValue ならば ArgumentOutOfRangeException をスローします。
範囲が広い場合に確率が偏る
範囲が狭い maxValue - minValue <= int.MaxValue のときは NextDouble() * (maxValue - minValue) + minValue を返すので、 Next(int maxValue) と同様です。
特筆すべきは maxValue - minValue > int.MaxValue の場合で、計算手法が異なります。前提として、元々の範囲より広い範囲に安直に変換すると絶対に出ない値が生じるなど、出力が偏ってしまいます。 (前述した浮動小数点数の丸め誤差とは別です。) 一番単純な例を挙げると、 0 <= x < 2L * int.MaxValue にしようとして x * 2 とすると全て偶数になってしまう、という感じです。余談ですが、この問題は 実際に PHP で発生しているようです (雑談の項を参照) 。
System.Random では、この問題を回避するために乱数を継ぎ足す処理が入っています。
maxValue - minValue > int.MaxValue の場合の等価なコードを示します。
int result = Next(); // 0 <= x < int.MaxValue if (Next() % 2 == 0) // ※均等ではない result = -result; // ※ 0 が出やすくなる。 -int.MaxValue < x < int.MaxValue double d = result; d += int.MaxValue - 1; // 0.0 <= x < 2.0 * int.MaxValue - 1 d /= 2u * int.MaxValue - 1; // 0.0 <= x < 1.0 return (int)((long)(d * ((long)maxValue - minValue)) + minValue);
上から順に難癖をつけていきます。
まず Next() % 2 == 0 ですが、前述したように Next() のパターン数は 個なので偏りが生じます。
1073741824 / 2147483647 (50.000000023283064 %) の確率で true 、 1073741823 / 2147483647 (49.999999976716936 %) の確率で false になります。
次に result = -result ですが、 0 を入れると値が変わらないことに気づけます。したがって、他の数値の 2 倍の確率で 0 が出現することになります。 (0 が概ね 、他は
程度になります。)
残りの d の計算については、 Next(int maxValue) の処理を 0.0 <= x < 2u * int.MaxValue - 1 の範囲で行うイメージです。ただし、ここでは逆数の乗算 d *= 1.0 / constant; ではなく除算 d /= constant; を使用しています。
この 2 つの演算はパッと見同じに見えますが、結果は異なります。具体的には、 Next(int.MinValue, int.MaxValue) で呼び出した際、 Next(int maxValue) の項で挙げた浮動小数点数の丸めによる誤差 (result != d * (maxValue - minValue) となる場合) が生じないようです。その代わり、除算なので多少遅くなりそうです。
double NextDouble()
0.0 <= x < 1.0 の double 値を返します。
等価な実装を示します。 (実際の実装は Sample() メソッドにあります。) Next(int maxValue) の計算で使われているものと同じです。
return Next() * (1.0 / int.MaxValue);
出力される最大値の誤記
0 より大きい最小の出力値は 4.6566128752457969E-10 ( 内部表現 0x3e000000_00200000 ) 、最大値は 0.99999999953433871 ( 0x3fefffff_ffc00000 ) になります。
MSDN には、取りうる最大値は 0.99999999999999978 ( 0x3fefffff_fffffffe ) であると書いてありますが、Next() が返す最大値を考えれば誤りであることは明らかです。
精度が低い
さて、 Next() の取りうる値は 種類ですから、
NextDouble() が取りうる値も同様に 種類となります。実際に
double の取りうる値の数と比べてみましょう。
double において、 0.0 <= x < 1.0 の範囲には 個の数値が存在します。 (
0.0 の内部表現は 0x00000000_00000000 、 1.0 の内部表現は 0x3ff00000_00000000 であることからわかります。) したがって、本来取りうる値の 程度しか埋められないことになります。だいぶ疎です。
最も、全領域をカバーするのは計算コスト的に割に合わないので、実用的には 52 ~ 53 bit 精度で妥協する場合が多いです。この 52 は、 double 型の仮数部の桁数 から来ています。 (+1 はケチ表現の分です。)
例えば、以下の手法では 53 bit 精度の double 値が得られます。
// ここでの Next() は ulong 型 (64bit) 全域のランダムな値を返すものとします return (Next() >> 11) * (1.0 / (1ul << 53));
何故素直に Next() * (0.5 / (1ul << 63)) としないのかというと、乗算の前に Next() が double にキャストされて結局 53 bit 精度になってしまうためです。
範囲加工における注意 - 最大値を含む可能性
Next() には範囲を指定するオーバーロードがありますが、 NextDouble() にはありません。
MSDN を見ると、以下の式で手動変換するとよい、とあります。
NextDouble() * (maxValue - minValue) + minValue
このコードには注意すべき点があります。 NextDouble() は 0 <= x < 1 なので、この式も minValue <= x < maxValue となりそうですが、 minValue の絶対値が大きく maxValue - minValue が相対的にかなり小さい場合などに x == maxValue となる場合があります。具体例としては (987654321, 987654444) が挙げられます。
余談ですが、Java の java.util.Random#doubles(double, double) では、このような場合に Math.BitDecrement() 相当のメソッドを使って 1 つだけ小さくすることで回避しているようです (実装)。
通常はあまり気にしなくても良いかと思いますが、 x == maxValue になるとゼロ除算や予期しない ∞ ・ NaN が発生しうる場合 (Math.Log() など) には注意が必要です。
NextBytes(byte[] buffer), NextBytes(Span<byte> buffer)
byte[] または Span<byte> 全域をランダムな値 ( 0x00 <= x <= 0xff ) で埋めます。 Span<byte> のほうは .NET Standard 2.1 から使えます。
等価な実装を示します。処理的にはどちらも同様に Next() の下位 8 ビットを使用して埋めていきます。
for (int i = 0; i < buffer.Length; i++) buffer[i] = (byte)(Next() & 0xff);
0xff が生成される確率が低い
さて、何度か述べたように Next() は 通りなので、
Next() & 0xff (言い換えれば Next() % 256) は均等になりません。 0xff が 8388607 / 2147483647 、それ以外はそれぞれ 8388608 / 2147483647 の確率となり、 0xff が出現する確率がわずかに低くなります。
Next() 1 回あたり 1 byte しか利用しない非効率な実装
本来 4 byte に近い情報量のある Next() 1 回あたり 1 byte 分しか生成しない、とても効率の悪い実装となっています。 Next() の値域問題もあるので 4 byte フルに使うわけにはいきませんが、少なくとも 3 byte 分は使えるので 3 倍近く速くできそうな気がします。
外部実装・その他の問題
以上で System.Random に実装されているメソッドの紹介は終わりです。あとは MSDN などを見ながら、さらなる重箱の隅をつついてきます。
スレッドセーフではない
System.Random はスレッドセーフではありません。乱数生成のたびに内部状態を更新する必要があるので、それはそうです。
MSDN のマルチスレッド処理のサンプルを見ると、乱数を取得する箇所を lock ステートメントで囲って対応しています。
lock で囲む以外の対応策としては、スレッドごとに System.Random インスタンスを生成する手法があります。無理にロックしなくていいのでこちらのほうが速くなりそうな気がします。 (試せてはいませんが……)
ただ、前述したように初期状態のパターンが に限定される問題 (生成する乱数列のバリエーションが少ない、最悪衝突する可能性) があったり、.NET Framework ならより深刻なシードが同一になる問題があったりするので、難しいところがあります。 xoroshiro128+ などの
jump() や、 java.util.SplittableRandom の split() のようなものをサポートしていればこの辺りが解決できるのですが、残念ながら System.Random では非対応です。
再現が難しい / シリアライズできない
System.Random では、同じ乱数列を再現したい場合 new Random(int Seed) を使用することになります。しかし難点がいくつかあります:
- 内部状態の情報量
に対して、初期状態が
しかない
- シードだけを保存する場合、とりうる状態 (→出力される乱数列) がかなり制限される
- 途中から再開することができない
- 例えば、乱数を
個消費した実験の続きをしたい場合、もう一度
個消費しなければならない
- 例えば、乱数を
内部状態の保存 (シリアライズ) ができれば簡単に途中から再開できるようになりますが、 System.Random はそのままではシリアライズできません。内部状態は private フィールドで、属性も特についていないためです。 protected なら継承すれば合法的に触れたかもしれませんが…
リフレクションを使えばできないことはないですが、ちょっと面倒です。
保存すべきフィールドは int[] _seedArray, int _inext, int _inexp の 3 つです。以下に状態を読み書きするサンプルを示します。テストのために内部状態を適当に書き換えていますが、実際に保存用途に使う場合はスキップしてお好みの入出力コードを書いてください。
ただ private フィールドなので外部アクセスは本来想定外の操作であり、将来的な動作は一切保証されません。
var rng = new Random(); var bindingFlag = BindingFlags.NonPublic | BindingFlags.Instance; var stateField = typeof(Random).GetField("_seedArray", bindingFlag); var inextField = typeof(Random).GetField("_inext", bindingFlag); var inextpField = typeof(Random).GetField("_inextp", bindingFlag); // 内部状態からの読み込み var state = stateField.GetValue(rng) as int[]; // int[56] var inext = (int)inextField.GetValue(rng); var inextp = (int)inextpField.GetValue(rng); // 書き込みテスト用(次の出力で 0 が出るようにする + ラグ指定修正) state[2] = 12345; state[33] = 12345; inext = 1; inextp = 32; // 内部状態への書き込み stateField.SetValue(rng, state); inextField.SetValue(rng, inext); inextpField.SetValue(rng, inextp); Console.WriteLine(rng.Next()); // `0`
ところで、内部状態全体の保存が面倒だからと言って、シード値だけを保存して乱数のセーブポイントを通るたびに (頻繁に) new Random(seed) しなおすような実装はくれぐれも行わないようにしてください。繰り返しになりますが初期状態は パターンしかないので、出力列が著しく限定され、最悪の場合意図せず同一の乱数列を出力してしまう可能性があります。
拡張性
継承による実装の拡張
MSDN を見ると、 System.Random を継承して 別の擬似乱数生成器を実装したり 、NextBytes(byte[] bytes, int min, int max) などの追加メソッドを生やしたり する手法が紹介されています。
しかし、継承した場合もれなく System.Random の内部状態 280 byte がついてきます (実測値。実装によって変わるかもしれません) 。もし別の擬似乱数生成器を実装するなら無駄になってしまいます。
また、Sample() メソッドを上書きすれば大体 OK 、といったことが書かれていますが、 double ベースの計算になるので上述した問題が生じます。といってもすべての public メソッドが virtual なので、すべて自前実装で置き換えてしまえば問題はありません。
アルゴリズムを差し替えたり出力関数を柔軟に追加したりすることを考えると、 interface IRandom を定義しておいて、出力関数などは拡張メソッドにする (今なら interface のデフォルト実装でしょうか?) 手法が思いついたりしますが、 System.Random の実装当時 (.NET Framework 1.1 → C# 1.2) には拡張メソッドが存在しないのでダメです。歴史の重みです。
いくつかの擬似乱数生成器を実装している Math.NET Numerics を覗いてみると、擬似乱数生成器側は class RandomSource を基底として遷移関数と基礎的な出力関数を実装し、複雑な変換関数 (正規分布など) の実装は class Normal といった別クラスに分離して new Normal(new Xoshiro256StarStar()).Sample() といった感じで利用できるようにしているようです。これが綺麗な気がします。
各種分布への変換
正規分布への変換
上の項で分布の話が出たので、一様分布以外では多分最もメジャーな 正規分布 への変換についても触れておきます。
Java には java.util.Random#NextGaussian がありますが、我らが System.Random にはもちろん実装されていないので、自力で対応する必要があります。
ざっくり Polar Method で実装すると以下のようになります。
/// <summary> /// 平均 0, 標準偏差 1 の正規分布に従う独立な乱数のペアを取得します /// </summary> public (double x, double y) NextGaussian() { double u, v, s; do { u = random.NextDouble() * 2 - 1; v = random.NextDouble() * 2 - 1; s = u * u + v * v; } while (s >= 1 || s == 0); s = Math.Sqrt(-2 * Math.Log(s) / s); return (u * s, v * s); }
x, y は独立なので、どちらを使っても・ペアで使っても大丈夫です。1 つだけ要る場合は単に捨てればよいです。
もし平均と標準偏差を変えたければ returnValue * stdev + mean としてください。
正規分布への変換には Box-Muller Transform もありますが、Polar Method のほうが若干高速です。雑にベンチマークを取ったところ、手元の環境では Polar Method が 44.90 ± 1.041 ns 、Box-Muller Transform が 56.32 ± 0.702 ns (± は標準偏差) でした。 Box-Muller Transform の微妙な利点としては、工夫すると消費する乱数が 2 個固定になる点が挙げられます。また、より高速な実装手法として Ziggurat algorithm がありますが、テーブルが必要だったり実装が大変だったりするのでここでは取り上げません。大量に正規分布乱数が必要であれば検討するとよいと思います。
その他の分布への変換
Math.NET Numerics を活用するとよいと思います。 (丸投げ)
数学的な確率分布以外では、円|球 の 中|外周 にランダムに配置する計算が (特に Unity で) よく使われます。 こちらの説明が分かりやすいです。
シャッフル
MSDN のサンプル実装は非効率
コレクションの要素の順序をランダムに入れ替える「シャッフル」について検討します。
System.Random には組み込みのシャッフル関数は存在しません。ただ、 MSDN にはカードのシャッフルのサンプル実装があります。
var deck = new Card[52] { ... }; // シャッフル用インデックス var order = new double[deck.Length]; for (int i = 0; i < order.Length; i++) order = random.NextDouble(); // order をキーとして deck をソート Array.Sort(order, deck);
この手法には何点か問題があります:
NextDouble()の出力値が同じ要素が存在した (衝突した) 場合の動作が不定です。- MSDN の Array.Sort を見た限りではイントロソート (不安定) のようですので、衝突した場合どちらに偏るかは場合によります。
- ちなみに安定ソート (
Enumerable.OrderBy) なら確実に偏ります。元々先頭に近いほうが必ず前に来ます。
- ちなみに安定ソート (
- 直感的には奇跡でも起こらない限りあり得ないのでは、と思いそうですが、 誕生日のパラドックス より 54562 個程度の要素に対して実行すると概ね 1/2 の確率でどれかが衝突します。
- MSDN の Array.Sort を見た限りではイントロソート (不安定) のようですので、衝突した場合どちらに偏るかは場合によります。
- 時間的に非効率です。一般にソートの計算量は
ですが、より効率的に
でシャッフルする手法が存在します。
- 空間的に非効率です。同じ要素数の
double[]を確保する必要があります。
素直に Fisher-Yates シャッフル を実装しましょう。
例では直書きしましたが、 IList<T> の拡張メソッドにしたりすると便利です。
var deck = new Card[52] { ... }; for (int i = deck.Length - 1; i > 0; i--) { int r = rand.Next(i + 1); (deck[i], deck[r]) = (deck[r], deck[i]); }
副作用をなくして IEnumerable<T> に対応する場合は、 取り出し版のアルゴリズム で 0 ~ n - 1 の連番をシャッフルした配列を作成して、 source.ElementAt(randomArray[i]) といった感じで参照する手法が考えられます。
余談: ランダム値のソートによるシャッフルの注意点
話はそれますが、ランダムな値をキーとしてソートする場合、横着して以下のように書くと例外 (ArgumentException など) がスローされる場合があります。
// DANGER! Array.Sort(deck, (_, _) => random.Next(-1000, 1000));
そもそもソートは値を一定の順番に並べるためのものなので、比較するたびに大小が変わるような一貫性のない操作を行うと破綻してしまうためです。しかも性質が悪いのが「確実に例外がスローされるわけではない」点で、初回は成功したからといって油断していると後で刺されたりします。
爆発するかどうかはソートの形式によります。 (a, b) => Next() のように 2 引数を取って比較するもの (Comparison<T> や IComparer<T> をとるものなど) は危険で、ランダムに例外が投げられます。
対して、 a => Next() のように 1 引数をキーとして取るもの ( Enumerable.OrderBy(Func<TSource, TKey>) など) は、問題ないこともあります。内部実装として、メソッドを 1 回評価して配列などに格納 → デフォルトの比較関数でソート、というようになっていれば、比較自体は一貫して行えるため問題ありません。
乱数性テスト
出力列の品質、言い換えれば「出力列が乱数らしい振る舞いをしているか」を調べてみます。 遷移・出力関数の各所に問題があるのは今まで述べたとおりですが、テストを通しても検出できることを示す、という位置づけにします。
「テスト」は、出力された乱数列に統計的検定や構造解析を行うことで、何らかの乱数らしからぬ構造が見出せるか、を調べるシステムをいいます。「良い乱数であることを示す」よりは、「特定条件下で明らかに悪いことを示す」ようなイメージです。ただ、たくさんのテストを実施して問題が検出されなければ、品質が良い (真の乱数列に近い性質を持つ) とみなせそうです。 *6
PractRand のテストで速やかに失敗する
強力で汎用的な乱数性テストツールとしては PractRand が有力です。自動で複数種のテストをかけることができ、検出力が高く誤検知 (真の乱数を入力してもテストに失敗すること) もほぼありません。
私は PractRand でデフォルトの最大値である 32 TB の出力を検定し、 FAIL となるテストが 1 つも存在しないことを前提として擬似乱数の設計・選定を行っています。
今回は、より多くのテストを行う設定の -te 1 -tf 2 -tlmaxonly を指定しました。
出力には、 Next() では 32 bit 全域の出力ができないため NextBytes() 相当の実装を使用しました。大抵のテストツールでは基本的に 32 or 64 bit 全域を出力するメソッドがあることを前提としているので、そのままではテストにかけられないこと自体がとても厳しいです。というのも、この変換がテスト結果に影響を及ぼす可能性があるので、妥当かどうか微妙なところがあるのです…
結果を以下に示します。疑わしいテスト結果だけが表示されており、成功したテストは ...and から始まる行にまとめて書いてあります。結果は Evaluation のところに注目してください。雰囲気としては以下のような感じです。
usual: まれによくある- これはあまり問題になりません。別のシードでは起きなかったりする微妙なエラーです
suspicious: だいぶ怪しい- 大抵の場合次の length で
FAILします
- 大抵の場合次の length で
FAIL: 確実にアウト- 明らかに何らかの欠陥があります
テスト結果 (長いので折り畳み - クリックすると開きます)
RNG_test using PractRand version 0.94
RNG = .netrandom, seed = 0xb2540eef
test set = expanded, folding = extra
rng=.netrandom, seed=0xb2540eef
length= 32 megabytes (2^25 bytes), time= 2.7 seconds
Test Name Raw Processed Evaluation
[Low1/8]BCFN(0+1,13-5,T) R= +20.1 p = 4.8e-8 very suspicious
...and 936 test result(s) without anomalies
rng=.netrandom, seed=0xb2540eef
length= 64 megabytes (2^26 bytes), time= 14.9 seconds
Test Name Raw Processed Evaluation
[Low1/8]BCFN(0+1,13-5,T) R= +41.1 p = 2.9e-16 FAIL !
[Low1/8]DC6-6x2Bytes-1 R= +6.5 p = 4.7e-4 unusual
...and 1006 test result(s) without anomalies
rng=.netrandom, seed=0xb2540eef
length= 128 megabytes (2^27 bytes), time= 30.8 seconds
Test Name Raw Processed Evaluation
[Low1/8]BCFN(0+1,13-4,T) R= +79.5 p = 1.0e-34 FAIL !!!
[Low1/8]DC6-6x2Bytes-1 R= +8.7 p = 3.4e-5 mildly suspicious
[Low1/8]DC6-5x4Bytes-1 R= +8.9 p = 1.5e-5 mildly suspicious
...and 1078 test result(s) without anomalies
rng=.netrandom, seed=0xb2540eef
length= 256 megabytes (2^28 bytes), time= 48.0 seconds
Test Name Raw Processed Evaluation
[Low1/8]BCFN(0+0,13-3,T) R= +44.0 p = 1.2e-20 FAIL !!
[Low1/8]BCFN(0+1,13-3,T) R=+129.4 p = 4.8e-61 FAIL !!!!
[Low1/8]DC6-6x2Bytes-1 R= +14.5 p = 1.1e-7 very suspicious
[Low1/8]DC6-5x4Bytes-1 R= +20.1 p = 5.5e-13 FAIL
[Low1/32]FPF-14+6/16:cross R= +5.7 p = 4.8e-5 unusual
...and 1146 test result(s) without anomalies
rng=.netrandom, seed=0xb2540eef
length= 512 megabytes (2^29 bytes), time= 68.1 seconds
Test Name Raw Processed Evaluation
[Low1/8]BCFN(0+0,13-3,T) R= +91.4 p = 4.8e-43 FAIL !!!
[Low1/8]BCFN(0+1,13-3,T) R=+257.6 p = 1.0e-121 FAIL !!!!!
[Low1/8]DC6-6x2Bytes-1 R= +30.8 p = 4.1e-20 FAIL !!
[Low1/8]DC6-5x4Bytes-1 R= +36.5 p = 2.3e-24 FAIL !!
...and 1216 test result(s) without anomalies
rng=.netrandom, seed=0xb2540eef
length= 1 gigabyte (2^30 bytes), time= 96.9 seconds
Test Name Raw Processed Evaluation
BCFN(0+3,13-1,T) R= +11.4 p = 1.4e-5 mildly suspicious
BCFN(0+4,13-1,T) R= +13.0 p = 1.7e-6 suspicious
[Low1/8]BCFN(0+0,13-2,T) R=+388.0 p = 6.9e-198 FAIL !!!!!!
[Low1/8]BCFN(0+1,13-2,T) R=+465.4 p = 1.9e-237 FAIL !!!!!!
[Low1/8]BCFN(0+2,13-3,T) R= +18.9 p = 9.2e-9 very suspicious
[Low1/8]DC6-6x2Bytes-1 R= +57.2 p = 5.1e-32 FAIL !!!
[Low1/8]DC6-5x4Bytes-1 R= +62.9 p = 1.5e-35 FAIL !!!
[Low4/16]BCFN(0+2,13-2,T) R= +26.9 p = 2.5e-13 FAIL
...and 1286 test result(s) without anomalies
rng=.netrandom, seed=0xb2540eef
length= 2 gigabytes (2^31 bytes), time= 146 seconds
Test Name Raw Processed Evaluation
BCFN(0+3,13-0,T) R= +27.2 p = 4.7e-14 FAIL
BCFN(0+4,13-1,T) R= +28.3 p = 1.0e-14 FAIL
[Low1/8]BCFN(0+0,13-1,T) R= +1303 p = 2.3e-701 FAIL !!!!!!!
[Low1/8]BCFN(0+1,13-1,T) R=+819.6 p = 8.3e-441 FAIL !!!!!!!
[Low1/8]BCFN(0+2,13-2,T) R= +47.7 p = 5.7e-24 FAIL !!
[Low1/8]DC6-6x2Bytes-1 R=+110.9 p = 1.1e-52 FAIL !!!!
[Low1/8]DC6-5x4Bytes-1 R=+117.3 p = 2.9e-74 FAIL !!!!
[Low4/16]BCFN(0+2,13-1,T) R= +42.0 p = 4.8e-22 FAIL !!
[Low4/16]BCFN(0+3,13-1,T) R= +13.9 p = 5.8e-7 suspicious
...and 1359 test result(s) without anomalies
rng=.netrandom, seed=0xb2540eef
length= 4 gigabytes (2^32 bytes), time= 241 seconds
Test Name Raw Processed Evaluation
BCFN(0+3,13-0,T) R= +57.5 p = 2.8e-30 FAIL !!!
BCFN(0+4,13-0,T) R= +50.5 p = 1.6e-26 FAIL !!
[Low1/8]BCFN(0+0,13-1,T) R= +2589 p = 1e-1393 FAIL !!!!!!!!
[Low1/8]BCFN(0+1,13-1,T) R= +1659 p = 9.2e-893 FAIL !!!!!!!
[Low1/8]BCFN(0+2,13-1,T) R= +82.8 p = 4.8e-44 FAIL !!!
[Low1/8]BCFN(0+4,13-2,T) R= +10.7 p = 4.6e-5 unusual
[Low1/8]DC6-6x2Bytes-1 R=+204.2 p = 6.8e-109 FAIL !!!!!
[Low1/8]DC6-5x4Bytes-1 R=+219.3 p = 1.7e-100 FAIL !!!!!
[Low1/32]BCFN(0+6,13-4,T) R= +12.2 p = 2.9e-5 unusual
[Low4/16]BCFN(0+2,13-1,T) R= +89.6 p = 1.0e-47 FAIL !!!
[Low4/16]BCFN(0+3,13-1,T) R= +24.5 p = 1.1e-12 FAIL
...and 1433 test result(s) without anomalies
rng=.netrandom, seed=0xb2540eef
length= 8 gigabytes (2^33 bytes), time= 497 seconds
Test Name Raw Processed Evaluation
BCFN(0+3,13-0,T) R=+115.8 p = 2.0e-61 FAIL !!!!
BCFN(0+4,13-0,T) R= +88.9 p = 4.5e-47 FAIL !!!
[Low1/8]BCFN(0+0,13-0,T) R= +5800 p = 9e-3101 FAIL !!!!!!!!
[Low1/8]BCFN(0+1,13-0,T) R= +2740 p = 8e-1465 FAIL !!!!!!!!
[Low1/8]BCFN(0+2,13-1,T) R=+169.1 p = 1.7e-90 FAIL !!!!!
[Low1/8]BCFN(0+4,13-1,T) R= +15.6 p = 7.9e-8 very suspicious
[Low1/8]DC6-6x2Bytes-1 R=+386.9 p = 1.0e-179 FAIL !!!!!!
[Low1/8]DC6-5x4Bytes-1 R=+415.2 p = 1.1e-253 FAIL !!!!!!
[Low4/16]BCFN(0+2,13-0,T) R=+156.1 p = 5.4e-83 FAIL !!!!
[Low4/16]BCFN(0+3,13-0,T) R= +34.5 p = 5.3e-18 FAIL !
...and 1530 test result(s) without anomalies
rng=.netrandom, seed=0xb2540eef
length= 16 gigabytes (2^34 bytes), time= 976 seconds
Test Name Raw Processed Evaluation
BCFN(0+3,13-0,T) R=+234.3 p = 8.5e-125 FAIL !!!!!
BCFN(0+4,13-0,T) R=+172.1 p = 1.4e-91 FAIL !!!!!
BCFN(0+6,13-0,T) R= +12.4 p = 3.6e-6 unusual
[Low1/8]BCFN(0+0,13-0,T) R=+11611 p = 1e-6207 FAIL !!!!!!!!
[Low1/8]BCFN(0+1,13-0,T) R= +5513 p = 2e-2947 FAIL !!!!!!!!
[Low1/8]BCFN(0+2,13-0,T) R=+273.9 p = 5.6e-146 FAIL !!!!!
[Low1/8]BCFN(0+3,13-0,T) R= +9.6 p = 1.1e-4 unusual
[Low1/8]BCFN(0+4,13-1,T) R= +22.3 p = 1.7e-11 VERY SUSPICIOUS
[Low1/8]DC6-6x2Bytes-1 R=+735.4 p = 1.2e-265 FAIL !!!!!!
[Low1/8]DC6-5x4Bytes-1 R=+780.1 p = 6.6e-429 FAIL !!!!!!!
[Low4/16]BCFN(0+2,13-0,T) R=+342.4 p = 1.2e-182 FAIL !!!!!!
[Low4/16]BCFN(0+3,13-0,T) R= +70.4 p = 3.7e-37 FAIL !!!
...and 1625 test result(s) without anomalies
64 MB まで検定した時点で BCFN テストに、 256 MB から DC6 テストに FAIL しました。ほぼ瞬殺です。
無事失敗したのと時間がかかるのとで 16 GB で中断しました。
参考として他の擬似乱数生成器はどうなのかというと、有名どころとしては線形合同法 (LCG) ・ Mersenne Twister ・ Xorshift ・ xoroshiro128+ は FAIL していて、PCG ・ xoshiro256** ・splitmix (≒ java.util.SplittableRandom) は 32 TB でもパスしています。 詳しくは こちら の "Failed Test" 列を参照してください。 hwd 以外は PractRand のテストです。
Hamming-weight dependencies
次に、xoroshiro/xoshiro の作者が作った Hamming-weight dependencies テスト (略称 hwd) *7 を試してみます。これは TinyMT において BRank 系以外のテストで初めて問題を検出できた実績のあるテストです。こちらは 1 PB (ペタバイト!) テストして p < 1e-20 にならなければパスしたといえます。
こちらでは試しに Next() 相当の実装を使用しました。また、HWD_BITS=32 (出力のワードサイズが 32 bit) としました。
結果の一部を以下に示します。本項執筆時点では 25 TB まで検定して p = 0.761 なので、意外なことに問題は検出されていなさそうです。最後までやると 2-3 週間ぐらいかかるのでこの辺りで許してください…
mix3 extreme = 1.51920 (sig = 00000100) weight 1 (16), p-value = 0.89 mix3 extreme = 2.67035 (sig = 00010010) weight 2 (112), p-value = 0.573 mix3 extreme = 3.41468 (sig = 00101200) weight 3 (448), p-value = 0.249 mix3 extreme = 3.23865 (sig = 12002010) weight 4 (1120), p-value = 0.74 mix3 extreme = 3.64975 (sig = 12222100) weight >=5 (4864), p-value = 0.721 bits per word = 32 (analyzing bits); min category p-value = 0.249 processed 2.5e+13 bytes in 4.14e+04 seconds (0.604 GB/s, 2.174 TB/h). Sun Jan 3 00:05:51 2021 p = 0.761 ------
ジャンプ
ジャンプ機能がない
擬似乱数生成器によっては、「ジャンプ」機能を備えているものがあります。
具体例を挙げると、 xoroshiro128+ では 回の
next() 呼び出しと等価な操作を速やかに行うことができる jump() 関数が用意されています。
この機能は並列実行などで複数の乱数列が必要な場合に便利で、 new Random() ではなく var child = original.Jump(); のようにしてインスタンスを生成することで、先の例でいえば 回
next() を呼び出すまでは重複しない保証のある乱数列を得ることができます。
さて System.Random ではどうなのかというと、少なくとも用意はされていません。設計するのもなかなか難しそうな気がします。 上での多項式計算を頑張ればできるかもしれませんが、
Next() の項で述べたように原始か分からなかったり、そもそも計算がよくわからなかったりするので私は何も分かりません。
余談: 「正しく」実装されていた場合のジャンプの設計
注記: 例によって
System.Randomには直接適用できません。
また机上の空論になってしまいますが、もしラグ指定が正しく法も 2 のべき乗である だったのならば、限定的ながら可能です。
先に述べたように、 ならば最下位ビットだけを見ると LFSR として扱うことができます。 LFSR でのジャンプ手法を用いることで、「少なくとも
ステップ以上の距離がある状態」を作り出すことが可能です。「少なくとも」というのは最下位ビット以外については制御できないためで、実際の距離は
という感じになると思います、たぶん…
LFSR のジャンプは、 を事前に計算しておいて (
は遷移関数の特性多項式です) 、実行時に
の
に現在の状態を代入することで行います。
例えば、
ステップのジャンプ多項式
は、 xoroshiro128+ の
JUMP[] と同じフォーマットなら 0x0010010010200200 として表せます。あとは xoroshiro128+ の jump() と同じ雰囲気で実装すれば少なくとも ステップ以上の距離がある状態を作り出すことができます。
ただ、変わるのは最下位ビットだけなので、この手法だけでは出力自体はしばらく元の出力列とほとんど同じになることが予想されます。難儀です。 とっても雑に見積もると、キャリーが 1 bit 上に伝播するのに 1 周かかる (= 55 回) x 31 bit なので 1705 回ぐらい乱数を読み飛ばすことで目に見える相関はなくなりそうな気がします。 (気がするだけで確たる根拠はないです…) もちろん重い処理なので手軽ではないですが…
「ガチャシミュレーション」における異常な振る舞い
本項の検討は、 dotnet/runtime の Issue #40490 およびオリジナルの StackOverflow への投稿 に基づきます。 ここまでの問題は誤差レベルのものが多かったですが、これは実用的なユースケースで目に見える問題が生じます。
System.Random を用いて、単発で確率 で当たるガチャを当たるまで引く (!) とき、最初に当たるまでに引いた回数
はどんな分布になるかのシミュレーションをしてみましょう。数学的には 幾何分布 というらしいです。
以下のように実装してみます。ガチャで当たるまでの回数の分布を、100 万回ぐらいシミュレーションしてみます。
var rand = new Random(); double p = 0.05; // 当たる確率 var distribution = new int[256]; // (i + 1) 回目で初めて当たりを引いた回数 for (int i = 0; i < 1 << 20; i++) { int done = 0; // 引いた回数(-1) while (rand.NextDouble() >= p) // 当たるまで回す!! done++; distribution[Math.Min(done, distribution.Length - 1)]++; } // 出力 for (int i = 0; i < distribution.Length; i++) Console.WriteLine($"{i + 1,3}: {distribution[i]}");
結果をグラフに書くと以下のようになります。
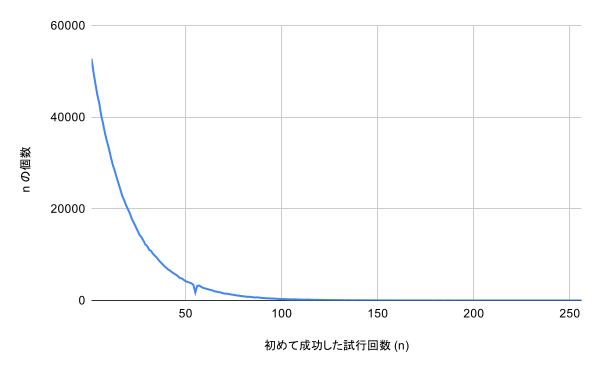
55 (回目に引いたときに初めて当たった回数) に不自然なピークがあるのが分かります。拡大して見てみましょう。ここで、追加の「理論値」は幾何分布の確率質量関数から求めています。

あるべき数の大体 1/2 ぐらいになっていそうです。なお、この現象は確率 に依存せず発生するようです。
原因を考えてみましょう。
遷移関数についての今までの説明から、55 回目の遷移・出力は と表せます。確率
は簡単のため整数で定義することとし、
として
のときに「成功」とします。
まず、式中の がとりうる値の範囲を考えます。
については、「55 回目に初めて成功した」すなわち「54 回目まではすべて失敗した」前提条件から、
です。
は、現在の 55 回前ですから「直前の試行の最後の出力」を指します。 (一番最初の試行でない限り) 最後は成功で終わっているので、
です。
以上の条件下で を満たすには、
である必要があります。ここで
を足したのは mod を打ち消すためです (
の値域から、
は必ず負値になります) 。 この 3 つの関係式を満たす
ペアの個数は
個となります。
の範囲条件を満たすペアの総数 (上記関係式は満たさなくてもよい場合) は
個ですから、この範囲内で成功する確率は
となります。本来の確率は
ですから、
がある程度小さければ本来の確率の大体 1/2 ぐらいになり、実験と一致しそうです。
イメージしやすいように図に描いてみましょう。 全域 (グラフ全体) に対して、
を満たすのは赤い部分です。色が濃い部分が成功、薄い部分は失敗を表します。 (色が濃い部分 / グラフ全体) に対して、 (赤色の濃い部分 / 赤色全体) の割合が半分ぐらいになっているのが分かるかと思います。

さて、原因は分かったので対策を考えてみましょう。直前の試行の最後の出力を参照して となっている、すなわち直前の試行の影響を受けているのがよくないので、例えば試行が終わった直後にランダムな個数だけ乱数を消費してみるのはどうでしょうか。あまり行儀は良くないですがサンプルということで許してください…
// 抜粋 for (int i = 0; i < 1 << 20; i++) { int done = 0; // 引いた回数(-1) while (rand.NextDouble() >= p) // 当たるまで回す!! done++; distribution[Math.Min(done, distribution.Length - 1)]++; // 追加コード: ランダムに 0 - 255 個消費する int skipAmount = Guid.NewGuid().ToByteArray()[15]; for (int k = 0; k < skipAmount; k++) rand.Next(); }
結果をグラフに書くと以下のようになり、本項の現象がみられなくなっています。

一応補足ですが、乱数の消費回数を決定するのに rand.NextInt(256) を使わなかったのには理由があります。自分自身の乱数を使用すると乱数列が重複する可能性が上がってしまうためです。
説明を簡単にするために 1 byte のカウンタを擬似乱数生成器と言い張ることにしましょう:
int rand() => (x = (x + 1) % 256);
ここで、 x == 128 のときは rand() => 129 となるので 129 回消費して x == 2 になります。また、 x == 0 のときは rand() => 1 となり 1 回消費して x == 2 になります。これらより、別の内部状態からランダムスキップによって同じ内部状態になってしまい、以降の出力列が重複してしまうことが分かります。 rand() とは関連性のない別系列の乱数 (ここでは Guid.NewGuid() の最後のバイト) を用いることで、この問題を回避している、というわけです。
話を戻してまとめに入ります。遷移・出力関数の実装がシンプルなため、「内部での状態更新処理」と「外部での乱数の利用処理」が嚙み合ってしまった場合このように問題が表出します。とはいえ「内部処理を把握したうえで注意して書け」というのは現実的ではありません。強いて対策を挙げるとすれば、別の擬似乱数生成器を採用するなどでしょうか……?
乱数列の過去と未来を知る
未来の予測 (内部状態復元攻撃)
出力から内部状態を復元して、将来の乱数の予想を試みます。
一番簡単な Next() について検討します。
Next() では内部状態をそのまま返しているので、連続する 55 個の出力列を記録できれば、それがそのまま内部状態 _seedArray になります。あとは _inext = 0; _inextp = 21; としてインスタンスに設定すれば出力列が再現できます。
// コピー元 var rand = new Random(); // 出力の記録 (内部状態に合わせるため [0] は飛ばす) int[] output = new int[56]; for (int i = 1; i < output.Length; i++) output[i] = rand.Next(); // クローンの生成・設定 var clone = new Random(); SetInternalState(clone, output, 0, 21); // 検証 for (int i = 0; i < 256; i++) Debug.Assert(rand.Next() == clone.Next()); // --- // リフレクションで内部状態を設定する static void SetInternalState(Random rng, int[] state, int inext, int inextp) { var bindingFlag = BindingFlags.NonPublic | BindingFlags.Instance; var stateField = typeof(Random).GetField("_seedArray", bindingFlag); var inextField = typeof(Random).GetField("_inext", bindingFlag); var inextpField = typeof(Random).GetField("_inextp", bindingFlag); stateField.SetValue(rng, state); inextField.SetValue(rng, inext); inextpField.SetValue(rng, inextp); }
また、もし内部状態全域が分からなくとも、遷移式 より 55 回前と 34 回前の出力を得ることによって、次に出力される値を求めることができます。
NextDouble() の場合は、 (int)Math.Round(value * int.MaxValue) などで整数に逆変換すれば、 Next() と同じ手法が適用できます。
その他の範囲に加工するもの (Next(int maxValue), NextBytes など) を情報源として内部状態の完全な復元を行う手法については、パッとは思いつきません。Lagged Fibonacci 法に対して適用できるアルゴリズムがあれば、それが使えるかもしれません。
別の手法としては、初期状態が高々 パターンしかないことから、同じ乱数列を出力する系列を
パターンの中から力ずくで探索する手法が挙げられます。初期化してからそれほど使用されていない (
Next() 呼び出し回数が少ない) と推測される場合に特に有効です。
また、 .NET Framework では初期化は起動時間ベースなので、全空間を探索しなくともある程度絞り込むことができます。例えば、初期化タイミングが 1 分オーダーでも分かっているなら、 60000 (ms) 個分試せばどれかは当たるでしょう。
過去の状態・出力列の逆算
Next() の逆演算 (直前の状態に戻す演算) を考えてみましょう。これが分かると、ある時点での内部状態が判明した際、過去の状態 (乱数列) の逆算ができます。
難しいことは何もなく、減算を加算にしてインデックスを戻す処理を書くだけです:
uint prev = (uint)_seedArray[_inext] + (uint)_seedArray[_inextp]; if (prev >= int.MaxValue) prev -= int.MaxValue; _seedArray[_inext] = (int)prev; if (--_inext <= 0) _inext += 55; if (--_inextp <= 0) _inextp += 55;
均等分布次元
System.Random の「均等分布次元」について考えてみましょう。よく Mersenne Twister の説明で「623 次元に均等分布する」と言われているアレです。
前提: 均等分布次元とは
そもそも均等分布次元とは何かというと、雑に説明すると「要素数 n の配列を連続する乱数で埋めたとき、全てのパターンが出現しうる最大の n」です。 623 次元に均等分布する Mersenne Twister では、 int[623] の配列を連続する Next() で埋めるとき、 int[623] で表現できるありとあらゆるパターンが出現しうることが保証されています。
この性質は当たり前に存在するわけではありません。例えば線形合同法は 1 次元均等分布なので、 int[2] ですらごく限られたパターンしか生成できません。より具体的には、以下の線形合同法では [0] = 0 なら [1] = 2531011 以外にはあり得ません。 それ以外の 0 から始まるベクトル ({0, 1} など) は絶対に生成されません。
線形合同法でランダムな 3 次元の点をプロットすると平面上に並ぶ 、というのは有名な話です。
uint lcg(uint x) => x * 214013 + 2531011;
System.Random の均等分布次元
話を戻して、 System.Random ではどうでしょうか。
そもそも遷移関数の実装ミスによって周期決定すらおぼつかない状態なので、実際の均等分布次元を求めることは困難です。はい……
ただ、もしも 上で
が原始多項式であり、最長周期を実現できていたなら 55 次元に均等分布します。
(各要素の値域は変わらず
であることに注意は必要です。)
証明といえるほど厳密ではないですが説明しましょう。
最長周期 を実現できているなら、内部状態は 全 0 を除いて全ての表現可能な状態を取ることができます。 (表現可能な状態のパターン数は最長周期と同じ数になります。) なお、全 0 は擬似乱数生成器の構造的にどうしようもないので見なかったことにします。 Mersenne Twister の論文 *8 の k 次元均等分布の定義 (Definition 1.1.) においても "except for the all-zero combination that occurs once less often." と述べられており、例外と考えてよいと思います。
そして、要素数 55 の内部状態と連続する 55 個の出力は一対一に対応します (全単射) 。言い換えれば、内部状態→出力 の逆となる 出力→内部状態 の変換を行えます。 具体的に以下のコードを用いて、連続する 55 個の出力から対応する内部状態を求められます。
// note: output.Length == 55, 0 <= output[i] < int.MaxValue static int[] OutputToState(int[] output) { if (output.Length != 55) throw new ArgumentException(nameof(output)); const int Lag = 34; // 55 - inext の初期値(21) var state = new int[56]; int index, laggedIndex; // == inext, inextp for (index = 55, laggedIndex = index - Lag; index > Lag; index--, laggedIndex--) { state[index] = output[index - 1] + output[laggedIndex - 1]; if (state[index] < 0) state[index] += int.MaxValue; } for (laggedIndex = 55; index > 0; index--, laggedIndex--) { state[index] = output[index - 1] + state[laggedIndex]; if (state[index] < 0) state[index] += int.MaxValue; } return state; }
内部状態がすべての可能な値を取ることと、内部状態と連続する出力は一対一対応することから、連続する 55 個の出力もすべての可能な値を取るといえます。したがって、55 次元に均等分布するといえます。
余談: 好きな「乱数」列を出力させる
さて、上の項で 内部状態⇔出力列 の計算が可能であることを示しました。ということは、欲しい出力列に対応する内部状態を設定することで、55 個までの範囲で好きな値を出力させることができます。
上の OutputToState() メソッドを利用して、文字列を仕込んでみました。
実行例を以下に示します。
var rand = new Random(1); var state = new int[] { 0, 292, 414, 406, 405, 358, 194, 456, 327, 414, 354, 401, 419, 347, 183, 304, 247, 303, 251, 236, 334, 307, 257, 330, 302, 300, 243, 162, 347, 226, 299, 239, 304, 316, 246, 151, 185, 150, 188, 219, 137, 220, 206, 160, 568, 602, 619, 558, 247, 530, 441, 537, 380, 440, 553, 443 }; // リフレクションで _seedArray, _inext, _inextp を設定する SetInternalState(rand, state, 0, 21); var randomBytes = new byte[128]; rand.NextBytes(randomBytes); // randomBytes を ASCII とみなして文字列化 Console.WriteLine(new string(randomBytes.Select(i => (char)i).ToArray())); // > output: // > OEEO@aAe?IU?#This message was created by Andante.Shioi-chan kawaii#AsS?oE2uo
# で囲まれているところが仕込んだ文字列です。 (# も含めて計 55 文字ジャストです。)
前述した Prev() を併用すれば、一定時間後に吐き出すような仕込みも可能です。
パフォーマンス
速度
パフォーマンスといえばまずは速度です。とりあえずベンチマークを取ってみましょう。 今回は BenchmarkDotNet を使用し、.NET 5 環境で測定しました。
BenchmarkDotNet=v0.12.1, OS=Windows 10.0.19042 Intel Core i7-7700HQ CPU 2.80GHz (Kaby Lake), 1 CPU, 8 logical and 4 physical cores .NET Core SDK=5.0.101 [Host] : .NET Core 5.0.1 (CoreCLR 5.0.120.57516, CoreFX 5.0.120.57516), X64 RyuJIT DefaultJob : .NET Core 5.0.1 (CoreCLR 5.0.120.57516, CoreFX 5.0.120.57516), X64 RyuJIT
せっかくなので、比較対象として拙作 Seiran128 擬似乱数生成器を使います。PractRand 32 TB をパスする品質を持ち、けっこう高速です。また、new() では RNGCryptoServiceProvider ベースの初期化を行ったり、 NextInt(int max), NextInt(int min, int max) では偏りがなくなるように操作を行ったりなど、速度を多少犠牲にしてでも品質を維持するように実装しています (つまり、速度だけ見てチューンするなら改善の余地がある、ということです) 。
Seiran 側の実装はこちら です。
各メソッドについて、処理時間は以下のようになりました。± は標準偏差です。
| Method | System.Random [ns] | Seiran [ns] | x Speed |
|---|---|---|---|
new() |
1741.159 ± 23.02 | 120.738 ± 1.079 | 14.421 |
new(401) |
470.529 ± 6.842 | 8.185 ± 0.087 | 57.487 |
Next() |
9.093 ± 0.113 | 1.330 ± 0.054 | 6.837 |
Next(401) |
11.748 ± 0.169 | 3.272 ± 0.039 | 3.590 |
Next(168, 401) |
11.473 ± 0.138 | 4.567 ± 0.063 | 2.512 |
NextDouble() |
9.734 ± 0.125 | 2.376 ± 0.034 | 4.097 |
NextBytes(Span<byte>[256]) |
2254.480 ± 27.31 | 90.324 ± 1.177 | 24.960 |
雑にグラフにすると以下のようになりました。 (グラフガチ勢に刺されそうです…)

Next***() がつぶれているので拡大するとこのようになります。

上表を見ると、new Random() が予想以上に遅いです。シード指定のある new Random(401) の 3.7 倍も遅いところを見ると、前述したシードが重複しないようにする処理が思いのほか重いのでしょうか。暗号論的擬似乱数生成器による初期化より遥かに遅いとはいったい… .NET Framework 環境ではほぼ new Random(401) と同じになるとは思いますが、ビルド環境がなかったので試せていません。
Seiran と比べると、出力系メソッドでは 2 ~ 4 倍 (NextBytes は 25 倍ぐらい) 、new では 14 ~ 57 倍 (!) ほど遅いことになります。
Seiran.NextBytes が速いのは、 MemoryMarshal.Cast() を使って直接 ulong の値を書き込んでいる (一度に 8 byte 分書き込める) ためです。C 言語でいうと ((uint64_t *)bytes)[i] = Next(); の処理をしているイメージです。対して Random.NextBytes は 1 byte / 回なので、かなりの差が付きます。
メモリ
消費メモリの観点からも見てみましょう。ゲーム分野などではヒープアロケーションに敏感になっている場合があるので、知っておいて損はないでしょう。
System.Random は、.NET 5 環境において 1 インスタンスあたり 280 byte 消費します。これは Visual Studio の診断ツールで確認しました。
加えて、一度でも new Random() を呼べば追加で 560 byte 消費します。これはちょうど 2 インスタンス分で、new Random() の項で述べた ThreadStatic なインスタンスと static なインスタンスによるものと思われます。
ちなみに、Seiran では 1 インスタンスあたり 32 byte で済みます。 (内部状態を配列で持つと 64 byte になります。)
本質的には 16 byte 分なのでワンチャン構造体にできるかもしれませんが、今回はそこまでしませんでした。
おわりに
調べれば調べるほど問題や変な性質が見つかるので、何か楽しくなって調べていたら 1 ヵ月が経っていました。誤差レベルのものもあれば、結構影響のあるものもあります。
「だから System.Random は使うな!!!!」といった強い言葉を使うつもりはないですが、ゲームの内部計算・科学シミュレーションといった繊細な用途に使用する場合は、問題が表出する可能性があるため注意が必要だと思います。特に、再現性が必要な場合は流石にやめておいたほうが良いかと思います (前言撤回) 。問題が起きても後で交換できなくなりますので……
対して、品質を気にする必要がなく、かつ再現性が不要な場合なら雑に使ってもよいかとも思います。ゲームで言えばパーティクルの飛ばし方などでしょうか。いくら品質が低いといえども、全力で偏ったりはしないのである程度の使用なら大丈夫です。 また、他では真似できない最強の利点が「標準ライブラリなのでいつでもどこでも簡単に使えること」です。適切に使っていきましょう。
さて、 dis るだけ dis って何もしないのもアレなので、ほぼ上位互換の代替実装を作ってみました。 (NextInt(0) が例外を投げるなど、厳密に互換性はないです。)
MIT License で公開します。テストは結構しましたが、何かバグがあったらごめんなさい。
Seiran128 sample implementation in C# (.NET 5)
最後の最後に免責事項です。それなりに調査したつもりではありますが、私は数学徒ではないので数学理論周りに誤りやずれがある可能性はあります。もし何かありましたら優しく指摘していただけると大変助かります。よろしくお願いします。
*1:全 0 などの周期が短い状態も含むため、実用的にはこれより小さくなります
*2:ラグの指定ミスは流石に意図したものではない、と信じているので…
*3: Brent, R. P. (1994). On the periods of generalized Fibonacci recurrences. Mathematics of Computation, 63(207), 389-401.
*4:Aviv Sinai. (2011) Pseudo Random Number Generators in Programming Languages. The Interdisciplinary Center, Herzlia Efi Arazi School of Computer Science.
*5:実際には Next(int minValue, int maxValue) があるためこのような操作はしないと思いますが
*6:厳密には「誤検知」や「テスト自身の妥当性」など若干難しいところはありますが、ここでは大目に見てください。
*7:Blackman, D., & Vigna, S. (2018). Scrambled linear pseudorandom number generators. arXiv preprint arXiv:1805.01407.
*8:Matsumoto, M., & Nishimura, T. (1998). Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Transactions on Modeling and Computer Simulation (TOMACS), 8(1), 3-30.
YouTube の動画をアラームにして、推しの声で目覚める
はじめに
私は VTuber をしばしば観る人なのですが、寝る前に「朝配信」の予約枠を開きっぱなしにしてアラーム代わりにすることで、快適に起床できた経験がありました。 (人の声が良い感じなのでしょうか…?)
しかしこの手法には、朝の時間帯に配信がないことが多い(特定の時刻ならなおさら)、配信者側が寝坊して一緒に寝坊する可能性もある、などの難点がありました。 *1
もちろん生配信を任意に開始することはできないので、アーカイブを適当に再生することでアラームにするプログラムを作成し、この問題の解決を図ります。
目標
- YouTube のプレイリストを取得する
- 指定された時刻になったら、プレイリストからランダムに動画を選択し、再生する
- 一日で動くところまで実装できる
という感じの、とりあえず動くクライアントプログラムを作成します。
実装(インストール手順)
YouTube の情報にアクセスする API のライブラリが幸い C# (.NET) に対応していたので、使い慣れている C# (と WinForms) で作成することにします。開発環境は Visual Studio 2019 です。 とりあえず動く目標で作ったので汚いのはご容赦ください…
https://github.com/andanteyk/YouTubeAsAlerm

なお、クライアントキーは安直に公開すると危ないということしか知らないので、自前で用意していただく方式としました。そしてキーをご用意できる方ならバイナリもビルドできるだろうということで、ソースのみの公開となります。 文字通りの日曜プログラミングの成果ですのでご容赦いただければ… あと万が一まずいものがあればこっそり教えてください…
また、YouTube のチャンネルを持っている(自分のプレイリストを追加・編集できる状態にある)ことが前提となります。
ビルド方法
インストール(ビルド?)方法とともに、開発で引っかかった点などを書いていければと思います。
まず、リポジトリを https://github.com/andanteyk/YouTubeAsAlerm.git から clone して Visual Studio で開き、プロジェクト→NuGet パッケージの管理からパッケージの復元を行います。YouTube API を使用するため Google.Apis.YouTube.v3 を使っています。
加えて、 YouTube のアカウント情報にアクセスするため、認証情報が必要になります。ビルドする前に以下の手順で認証情報を取得します。
認証情報の作成
※予防線:使用歴 6 時間の人間が書いています。以下手順でとりあえず動きますが、管理的に危険などあれば突っ込んでいただけると幸いです。
https://console.cloud.google.com/apis/dashboard にアクセスして、「プロジェクトを作成」します。 適当なプロジェクト名をつけて作成したら、「+ API とサービスの有効化」から「YouTube Data API v3」を選択して有効にします。
すると、以下のように表示されるので、
この API を使用するには、認証情報が必要になる可能性があります。開始するには、[認証情報を作成] をクリックしてください。
「認証情報を作成」します。
使用する API は先程追加した「YouTube Data API v3」, API を呼び出す場所は今回の用途的に「その他の UI (Windows, CLI ツールなど)」を選択します。 アクセスするデータの種類については、今回はプレイリストにアクセスしたいので「ユーザーデータ」とします。
すると、「OAuth 同意画面の設定」をしろと言われるので、設定します。
User Type は「外部」にします。 *2
次に、アプリ情報を適当に入力します。ガイドにあるように、同意画面(このアプリケーションによる操作を許可しますか?的な画面)でこれらの情報が表示されます。
次に、スコープ(許可される操作)を指定します。今回は「YouTube プレイリストの取得」だけできればよいので、 .../auth/youtube.readonly を追加して「保存して次へ」移動します。
次に、テストユーザの指定があるので、お使いの Google アカウント(使いたい YouTube チャンネルがあるアカウント)を登録します。削除はできないらしいので注意してください。(とはいえ、100 枠もあるのでひとりで使う分には問題なさそうです。)
以上が完了したら、元の「プロジェクトへの認証情報の追加」ページに戻ります。 OAuth 2.0 クライアント ID に適当なものを設定し、「作成」ボタンを押します。
以上が完了したら、「認証情報」画面に移動し、OAuth 2.0 クライアント ID から作成した項目のダウンロードボタンを押すと client_secret_<ClientID>.json ファイルが入手できます。これを認証に使います。
なお、このファイルは秘密なので、git リポジトリに含めたりしないよう十分注意してください。 私の理解の範囲では、API を無限に叩いてリミットを使い果たすとか悪いことをされる可能性があります。
以上で認証情報の取得が完了しました。
実行
アプリを一度ビルドした後、exe と同じ場所 (…/bin/Debug など) に先程の JSON ファイルを client_secrets.json にリネームして配置します。
実行すると初回はブラウザで認証画面が開くので、使いたいチャンネルを指定して許可してください。信用されていないので警告が出ますが、自分自身がユーザなので大丈夫だと思います。多分…
うまくいけばプレイリストが勝手に取得されるので、Alerm タブで適宜アラームを設定すれば、指定した時刻にプレイリスト内のランダムな動画がブラウザで開かれます。これで快適な朝が迎えられますね…?
あとは、開発で得られた知見(つまづきポイント)を書いていきます。
データ取得の流れ
Channels.List - チャンネル取得
Playlists.List - チャンネル内のプレイリスト取得
PlaylistItems.List - プレイリスト内の各項目(動画)取得
上から順に取得してサーチしていくイメージです。 具体的な処理は ApiManager.cs を参照してください。
後で見る (Watch Later) は取得できない
https://t.co/05evYD0uvs
— Andante (@andanteyk) 2020年12月13日
> As of Sep 12 2016, watch later and watch history can no longer be retrieved YouTube Data API v3.
ンンンンンン
「後で見る」のプレイリストは API から取得できないようです。元々の目標はこのリストから再生することだったので、最初から知っていれば実装しなかったかもしれません……
プレイリスト内容取得 API のリファレンス を見ると、確かに
forbidden (403)
watchLaterNotAccessible
Items in "watch later" playlists cannot be retrieved through the API.
とあります…
これが載っているのは英語版だけで、日本語版にアクセスすると書いていません。古い翻訳が残っている感じでしょうか… 軽くググった限りでもそこそこ差分があるようなので、英語版を翻訳して読んだほうがよさそうです。
非公開・削除済み動画を検出する
非公開・削除済みの動画が再生されるとアラームにならないので、ランダム再生から除外する必要があります。
公式のフラグは 3 秒で見つけられなかったので、サムネイルが存在するかどうかで判定しました。 *3
playlistItem.Snippet.Thumbnails.Standard == null なら、非公開か削除されている…はずです。
参考文献
https://developers.google.com/youtube/v3/getting-started
こんな記事を読まなくても、公式のドキュメントを見ると雰囲気で分かります。サンプルも充実しているのでとりあえず動かしてみることができます。(最新版のコードである保証はないですが…?)
https://developers.google.com/youtube/v3/docs
API リファレンスです。何が返ってくるかはこちらを参照してください。
おわりに
思っていたよりだいぶ簡単に YouTube の情報にアクセスできることが分かりました。
ここ 2 日ほど稼働試験してみていますが、普通のアラーム音より快適に起きられます。とりあえずお歌リストを突っ込んだところ、朝一番でイントロクイズを楽しむことができています。(?)
内容がだいぶ薄い感じなので参考になるか微妙ですが、インストール手順の記録がてら残しておきます。
.NET 標準ライブラリの新機能と、乱数生成における利用
はじめに
2020/11/10 に .NET 5 がリリースされました。 🎉
何気なく MSDN を見ていると、結構便利なメソッドがちょくちょく追加されていることに気づいたので、擬似乱数の実装(または、何らかの数学的処理や黒魔術)で役立ちそうなものを実例と合わせてピックアップして紹介します。加えて、古い環境で悲しみを背負った場合のために、代替実装もできる限り載せておきたいと思います。
普段が .NET Standard 2.0 だったり果ては .NET Framework 4.5.2 だったりする民なので、最新環境の方からすれば既知の情報が多いかもですがご容赦ください。 また、.NET 5 に限らず、比較的新しめ[要出典]の .NET Core 3.0 あたりで追加されたものについても取り上げていきます。
System.Math
数学ライブラリ System.Math にもいくつか追加があります。
BigMul (.NET 5)
public static ulong BigMul (ulong a, ulong b, out ulong low);
a * b を 128 bit で計算して、上位 64 bit (と out 引数で下位 64 bit) を返します。
使用例としては、 64 bit の乱数を 0 <= x < max の範囲に加工するときが挙げられます。
// Next() は ulong (64 bit) の乱数を返すものとします // [0, max) の乱数を得ます static ulong Next(ulong max) => Math.BigMul(Next(), max, out _);
どうしてこれが成り立つのかは、小数点以下 64 bit の固定小数点数に見立ててみると分かりやすいです。
Next() / 2^64 は 0 <= x < 1 となるので、それに max を掛ければ 0 <= x < max が得られるというわけです。上位 64 ビットだけ取り出すことで / 2^64 の部分と同じ効果が得られます。
*1
上の例のように、コストの重い除算や剰余算の代替として使える場合があります。 *2 そこそこ使う割に実装しようとすると面倒なので、標準で採用されて本当にうれしいです。
代替実装の例を以下に挙げます。 *3
public static (ulong lo, ulong hi) BigMul(ulong a, ulong b) { ulong ahi = a >> 32, alo = a & uint.MaxValue, bhi = b >> 32, blo = b & uint.MaxValue; ulong tlo = alo * blo; ulong thi = ahi * bhi; ulong tmid = (ahi - alo) * (blo - bhi); long carry = tmid == 0 ? 0 : (long)(ahi - alo) >> 63 ^ (long)(blo - bhi) >> 63; tmid += tlo; if (tmid < tlo) carry++; tmid += thi; if (tmid < thi) carry++; carry <<= 32; ulong lo = tlo + (tmid << 32); if (lo < tlo) carry++; ulong hi = thi + (tmid >> 32) + (ulong)carry; return (lo, hi); }
BitIncrement / BitDecrement (.NET Core 3.0)
public static double BitIncrement (double x);
public static double BitDecrement (double x);
指定した浮動小数点値の次に大きい・小さい値を返します。例えば 1 を渡すと、それぞれ 1.0000000000000002, 0.9999999999999999 を返します。
乱数生成のほうでは、例えば厳密に 0 <= x < max の範囲を求めたい際に計算誤差で x == max となってしまった場合に 1 つ小さくして x < max を保証する、といった使い方をします。 *4
今までは擬似 union でビットレイアウトを重ねることで、整数として +1/-1 してまた戻す、といった手法で実現していました。
[StructLayout(LayoutKind.Explicit)] internal struct DoubleUint64Union { [FieldOffset(0)] public double d; [FieldOffset(0)] public ulong i; } public static double BitIncrement(double d) { if (double.IsNaN(d) || double.IsInfinity(d)) return d; if (d == 0) return double.Epsilon; var conv = new DoubleUint64Union() { d = d }; if (d > 0) conv.i++; else conv.i--; return conv.d; } public static double BitDecrement(double d) { if (double.IsNaN(d) || double.IsInfinity(d)) return d; if (d == 0) return -double.Epsilon; var conv = new DoubleUint64Union() { d = d }; if (d > 0) conv.i--; else conv.i++; return conv.d; }
FusedMultiplyAdd (.NET Core 3.0)
public static double FusedMultiplyAdd (double x, double y, double z);
x * y + z を返します。いわゆる積和演算というものです。
一見存在意義が不明そうですが、通常の x * y + z が (t =) x * y と t + z の 2 回丸め処理が入るのに対し、このメソッドでは 1 回だけに抑えることができます。したがって等価な計算ではないため、互いに置き換えると結果が微妙に変わる場合があって注意が必要です。
実用的には、例えば 0.0 <= x < 1.0 の乱数を min <= x < max に加工する際に FusedMultiplyAdd(x, max - min, min) などとして使えます。
これについてはソフトウェア的に再現するのが面倒そうです。
他の言語で fma などとして使われているものを正しく移植する際にも役立ちそうです。
ScaleB (.NET Core 3.0)
public static double ScaleB (double x, int n);
x * 2^n を返します。こちらも効率的らしいです。 n には負値も指定できます。
実用的には、64 bit の乱数を 0.0 <= x < 1.0 の浮動小数点数に変換する際に使えそうです。
(ほぼ)等価な演算と合わせて例を載せます。
double NextDouble() => Math.ScaleB(Next() >> 11, -53); // double NextDouble() => (Next() >> 11) * (1.0 / (1ul << 53));
(ちなみに少し試した感じでは、結果はほぼ同じで後者のほうが若干速い気がしました… 環境によるのでしょうか…?)
System.MathF (.NET Core 2.1)
System.Math の float 版です。 Unity の UnityEngine.Mathf とは微妙に文字が違います…
float 版のメソッドを作成する際にキャストが不要になるため便利です。 (結構前からあったようですが気づきませんでした…)
System.BitConverter
Int32BitsToSingle / SingleToInt32Bits (.NET Core 2.0)
public static float Int32BitsToSingle (int value);
public static int SingleToInt32Bits (float value);
float ⇔ int の変換を行います。キャストと違うのは、 浮動小数点数のビット構造 をそのままコピーする点です。
例えば、 SingleToInt32Bits(1f) == 0x3f800000 となります。
今までは BitIncrement の項と同じように擬似 union で得ていました。
実用例としては、整数 (uint/ulong) の出力を浮動小数点数に変換する手法のひとつが知られています。
// returns 0f <= x < 1f float NextFloat() => BitConverter.Int32BitsToSingle(0x3f800000 | NextUint() >> 9) - 1f;
雑に解説すると、ビットパターン 0x3fxXXXXX (x = 8~f) は (1.xXXXXX * pow(2, 0))、すなわち 1.0f <= x < 2.0f となります。そこから 1 を引いて 0f <= x < 1f を得ています。
なお、double ⇔ long 版の Int64BitsToDouble, DoubleToInt64Bits は昔 (.NET Framework 1.1) から存在しました。なぜ double だけ…とか言いながら float 版の互換実装を用意する必要がなくなりました。
ところで、なぜ float ⇔ uint, double ⇔ ulong ではないのか、と思ったのは私だけではないと信じています… 完全に推測ですが CLS 準拠 のためかと思っています。
System.Buffers.Binary.BinaryPrimitives (.NET Core 2.1)
クラスの存在自体気づいていませんでした…
ReverseEndianness
public static ulong ReverseEndianness (ulong value);
(その他のプリミティブ型も同様)
バイトオーダーを逆転させます (いわゆる BSWAP です)。 0x0123456789abcdef ⇔ 0xefcdab8967452301 となります。
まれに BSWAP を使ったプログラムを書きたくなったときに便利そうです…? *5
今までは System.Net.IPAddress.HostToNetworkOrder (かその逆) の目的外使用をすることもあったかと思いますが、正式にこちらが使えそうです。ちなみに、普通に実装しようとすると以下のようになります。
ulong ReverseEndianness(ulong x) { x = (x & 0x00ff00ff00ff00ff) << 8 ^ (x >> 8 & 0x00ff00ff00ff00ff); x = (x & 0x0000ffff0000ffff) << 16 ^ (x >> 16 & 0x0000ffff0000ffff); return x << 32 ^ x >> 32; }
ちなみにちなみに、 ReverseEndianness(byte value) とかいう虚無も存在します。なにもしません。
このクラスには、これ以外にも ReadOnlySpan<byte> からそれぞれのエンディアンでプリミティブ型を読み込む・書き込むメソッドが用意されています。
System.Half (.NET 5)
16 bit の浮動小数点型です。精度を犠牲にするかわりに、スペースや処理負荷を軽減する際に使う用です。
今のところは別環境との相互運用のためにあるらしく、直接計算はできず、比較や float / double へのキャストのみが行えます。 導入の経緯については 公式のブログ に詳しいです。
ちなみに、まだ half ではありません。Half と大文字で書く必要があります。
おわりに
書き終わってみると .NET 5 より前に出ていた API が多いですね… アンテナが低いです…
この記事を要約すると Math.BigMul がうれしい になります。他にも Index/Range や Span, MemoryMarshal.Cast など、便利アイテムが続々追加されているので (例によって .NET 5 よりも前からあるものですが)、興味のある方は調べてみてください。
いつの日か Unity で使えることを願って……
*1:なお、この使い方は厳密には正しい分布が得られないことは注記しておきます。 max が 2 のべき乗でなければわずかに生成確率に偏りが生じます。偏らない改善手法などについては https://www.pcg-random.org/posts/bounded-rands.html が詳しいです。
*2:実測だとあまり変わらない場合もありますが…
*3:Karatsuba 法の勉強もかねて実装したのですが、安直に 4 回乗算する手法のほうがなぜか早くなってつらみを背負っています…?正直あまり自信がないので安直にやったほうがいい気もします
*4:C# ではないですが、Java の Random.doubles(double, double) の実装において見られます。
*5:擬似乱数の出力関数の設計をするときに使っていたことがありました。キャリーによる非線形性は上位ビットに集まりがちなので、これで上下を入れ替えてまんべんなく非線形にしよう、という狙いがありました。例えば bswap(s0 + s1) + s1 など。
Z3 Solver で擬似乱数の内部状態を復元する+α
はじめに
擬似乱数の出力列から内部状態を復元することができれば、未来予測が可能になります。 以前の記事 でその一部を紹介しましたが、その構造についてよく理解して解析する必要があるなど、手間がかかっていました。 ここでは、ツールを使っていい感じに問題を解いてもらう方法について紹介します。
Z3 Solver
Z3 は、Microsoft Research が開発している SMT ソルバです。 私もふんわり使用しているだけなので適当に説明すると、関係式をいくつか投入すると、それらの式が成立するか、もし成立するなら値が何のときか、といったことを求めてくれるプログラムです。例えば、
* x, y は自然数 * x + y == 5 * x >= 3 をすべて満たす x, y は存在するか?
に対して、
(x = 3, y = 2) のとき成立する
といった感じで答えが返ってきます。
様々な言語に対応しており、Readme 曰く python, C++, C#, Java などで使えます。
C# での利用
NuGet で Microsoft.Z3.x64 をインストールすれば使えるようになります。
実装例を以下に示します。これは上に挙げた例を実際にコード化したものです。
using (var context = new Context()) using (var solver = context.MkSolver()) { // 変数 x, y を定義 var x = context.MkIntConst("x"); var y = context.MkIntConst("y"); // 関係式 x + y == 5 を追加 solver.Assert(context.MkEq(context.MkAdd(x, y), context.MkInt(5))); // 関係式 x >= 3 を追加 solver.Assert(context.MkGe(x, context.MkInt(3))); // 式が成立するかを調べて、成立すればそれを出力 var issat = solver.Check(); Console.WriteLine(issat); if (issat == Status.SATISFIABLE) { Console.WriteLine(solver.Model); } }
実行すると以下の出力を得ました。計算できていることが分かります。
SATISFIABLE (define-fun y () Int 2) (define-fun x () Int 3)
なお、解が複数あったとしてもそのうちのどれか一つが得られます。今回で言えば (x = 4, y = 1) も条件を満たしますが、こちらは得られるとは限りません。
また、どうやっても成立しない場合は UNSATISFIABLE が得られます。
記述がつらい
上の例を見れば分かると思いますが、Z3 では関係式の記述はすべてメソッド context.Mk***() を通して行います。とてもつらいので、普通の式と同じように演算子を使って書きたくなります。
ということで、ちょっとしたラッパー RngSolver を実装しました。 RngSolver と書いてはいますが、乱数用途以外にも使えるかもです。
https://github.com/andanteyk/RngSolver
詳しくは SolveRng.cs を参照してください。
実用例
xoshiro256+ の内部状態復元
上述した RngSolver の SolveRng.cs をちょっといじって、 xoshiro256+ の内部状態復元を試みます。 解説コメントも適当に付け足しました。
public static void Solve() { // seed: 適当なシード値(正解) var seed = new ulong[] { 0x0123456789abcdef, 0xfedcba9876543210, (ulong)Environment.TickCount, (ulong)DateTime.Now.Ticks } .Select(s => new Arithmetic(s)).ToArray(); // outputs: 観測された出力 // 今回は検証目的なのでシードから実際に出力させて outpus を設定していますが、 // 実際に観測から復元するときは outputs に直接突っ込みます var outputs = new Arithmetic[seed.Length + 1]; { var clone = seed.Select(s => s.Identity()).ToArray(); for (int i = 0; i < outputs.Length; i++) outputs[i] = Next(clone) as Arithmetic; } Console.WriteLine($"start: {DateTime.Now:yyyy/MM/dd HH:mm:ss.fff}"); using (var context = new Context()) using (var solver = context.MkSolver()) { // state を変数として宣言 var state = Enumerable.Range(0, seed.Length).Select(i => new BitVecWrapper(context.MkBVConst("state" + i, 64), context)).ToArray(); // 「出力列 [Next(state), ...] が outputs と等しい」制約を設定 for (int i = 0; i < outputs.Length; i++) { var res = Next(state); solver.Assert(res.Equals(outputs[i]) as BoolExpr); } // したがって、outputs と同じ出力を生成する内部状態 state が得られる(かも) var issat = solver.Check(); Console.WriteLine(issat); if (issat == Status.SATISFIABLE) { Console.WriteLine(solver.Model); } } Console.WriteLine($"end : {DateTime.Now:yyyy/MM/dd HH:mm:ss.fff}"); } // RngSolver を使うと、以下のように関係式定義が簡潔に行え、 Mk***() 地獄を回避できます // ついでに ulong と BitVecExpr の計算を 1 つの定義で行えます // このメソッドを書き換えれば別の乱数の出力推測ができます public static IArithmetic Next(IArithmetic[] s) { var result = (s[0] + s[3]); var t = s[1] << 17; s[2] ^= s[0]; s[3] ^= s[1]; s[1] ^= s[2]; s[0] ^= s[3]; s[2] ^= t; s[3] = s[3].Rol(45); return result; }
実行すると以下が得られました。40 秒程度で、連続した 64 bit の出力 x 5 から内部状態を復元することができました。
start: 2020/12/05 00:18:56.258 SATISFIABLE (define-fun state3 () (_ BitVec 64) #x08d898b35ac76c8c) (define-fun state1 () (_ BitVec 64) #xfedcba9876543210) (define-fun state0 () (_ BitVec 64) #x0123456789abcdef) (define-fun state2 () (_ BitVec 64) #x00000000465512c4) end : 2020/12/05 00:19:32.102
ちなみになのですが、 xoshiro256+ は出力関数に + を用いて非線形な出力を行っています。 *1
そのため、生で吐き出す Xorshift や 出力関数が線形な MT19937 に対して有効な「行列計算を用いた内部状態復元」が適用できず、私が知る限りでは solver 利用が最速の手法となっています。
なお、復元できるかどうかは遷移関数や出力関数の複雑さに依存します。関数によっては n 時間かかったり、 n 日かかっても結果が出なかったりします。
x << 2 ^ x >> 19 の可逆性
以前話に出した、 long x; x << 2 ^ x >> 19 (>> は右算術シフトです) が逆算可能かどうか=可逆であるかを調べたいとします。
厳密には数学的に証明する必要がありますが、今回はソルバーでざっくり調べます。
全ての x に対して逆算可能である、と示すのは大変なので、逆算ができない x が存在しないことを求める方針で実装します。
例えば異なる a, b を入力として同じ結果 z が得られた場合、逆算 inv(z) の値が a, b の "どちらか" になってしまいただ一つに決定できなくなります。したがって、そのような a, b が存在すれば逆算不可能、存在しなければ逆算可能であるといえるでしょう。前の項とは逆に、成立不可能 UNSATISFIABLE であれば嬉しいわけです。
それをコードに落とし込んだのが Invertible.cs です。ちょっと改造・補足説明して、以下に示します。
public static void IsInvertible() { Console.WriteLine($"start: {DateTime.Now:yyyy/MM/dd HH:mm:ss.fff}"); using (var context = new Context()) using (var solver = context.MkSolver()) { // 上の説明で言う a, b を定義 var state = Enumerable.Range(0, 2).Select(i => new BitVecWrapper(context.MkBVConst("state" + i, 64), context)).ToArray(); // (a != b) かつ (f(a) == f(b)) を満たす (a, b) ? solver.Assert(state[0].NotEquals(state[1]) as BoolExpr); solver.Assert(Output(state[0]).Equals(Output(state[1])) as BoolExpr); // 成立しなければ逆算可能、成立すれば逆算不可能 var issat = solver.Check(); Console.WriteLine(issat); if (issat == Status.SATISFIABLE) { Console.WriteLine(solver.Model); } } Console.WriteLine($"end : {DateTime.Now:yyyy/MM/dd HH:mm:ss.fff}"); } // x << 2 ^ x >> 19 public static IArithmetic Output(IArithmetic s) { return s << 2 ^ s.Sar(19); }
これは速やかに UNSATISFIABLE を得ます。したがって、全ての入力に対して逆算ができることが示されました。
(しかしここでは具体的な逆算方法は得られません。自分の目で確かめてみてください。)
start: 2020/12/05 00:51:00.302 UNSATISFIABLE end : 2020/12/05 00:51:00.382
では、 x << 6 ^ x >> 19 はどうでしょうか。末尾の Output を書き換えて実行してみると…
start: 2020/12/05 00:53:05.689 SATISFIABLE (define-fun state1 () (_ BitVec 64) #x4b206621b61e1a1b) (define-fun state0 () (_ BitVec 64) #x4f206623b61e1b1b) end : 2020/12/05 00:53:05.778
SATISFIABLE を得ます。いわば「反例を得た」状態であり、入力を 0x4f206623b61e1b1b および 0x4b206621b61e1a1b とした場合の出力が一致するため、逆算ができない場合があることが示されました。
実際に計算すると同一の出力 0xc81981098b42b003 が得られます。
ついでに x << a ^ x >> b は全ての a, b において常に逆算できるわけではないことも分かりました。
おわりに
Z3 solver を用いることで、関係式しか知らない状態からでも条件を満たす値があるかどうかを調べることができました。 「なんかよくわからんが、とりあえず求められたら ヨシ!」という問題に対して、最初にぶつけてみるには非常に強力なツールだと思います。
ちなみに、python では最初からもうちょっと楽に使えるらしいです。私は残念ながら python 分からない人なので省略します。 公式のリファレンスも充実しており、Web 上で実際に実行できるチュートリアル なんてすごいものもあります。気になった方は一度見てみると楽しいかもしれません。
*1:+ は線形では?となるかもしれませんが、 の世界では加算は ^ (XOR) です
乱数を巻き戻す
はじめに
(ほぼ) 最大周期を実現している擬似乱数生成器は、状態を巻き戻す(逆方向に進める)ことができます。
例えば xoshiro256 が、以下のように一見ランダムな内部状態を持っていたとしましょう。
var state = new ulong[] { 0x010F4C454914CD78, 0x83A5678480A2B416, 0x2652B51299006A0A, 0x900FEBAD58D7C533 };
この状態は、5 回の遷移 (next() 呼び出し) を経て、綺麗に並ぶようになります。
var state = new ulong[] { 0x0123456789abcdef, 0xfedcba9876543210, 0xdeadbeefcafebabe, 0x1685819840150026 };
もちろんこれは偶然に任せて求めたわけではなく、最初に下の状態があって、そこから巻き戻して上の状態を求めています。 この記事では、どうやったら巻き戻す関数を設計できるか、を紹介します。
xoshiro256 を巻き戻す
まず、xoshiro256 の内部状態 state を次に進めるメソッド Next() のコードを示します。
遷移関数はもちろん 公式の実装 と同じです。出力はここでは不要なので返り値は void にしています。
*1
// ulong[] state = new ulong[4] {...}; public void Next() { ulong t = state[1] << 17; state[2] ^= state[0]; state[3] ^= state[1]; state[1] ^= state[2]; state[0] ^= state[3]; state[2] ^= t; state[3] = rotl(state[3], 45); // rotate left. } public static ulong rotl(ulong x, int k) => x << k | x >> -k;
先に答えを示しておきましょう。内部状態 state を巻き戻すメソッド Prev() のコードを示します。
public void Prev() { state[3] = rotl(state[3], 19); state[0] ^= state[3]; ulong t = state[1] ^ state[2]; state[1] = t ^ t << 17 ^ t << 34 ^ t << 51; state[3] ^= state[1]; state[2] ^= state[0] ^ state[1] << 17; }
どのようにして求めたか、順を追って説明していきます。
遷移を分かりやすくするため、遷移前の state を prev として保存しておき、それが Next() を通して次の state にどう反映されるかを見ます。
state の各要素について整理すると以下のようになりました。
public void Next() { // copy of initial `state` ulong[] prev = state.ToArray(); state[0] = prev[0] ^ prev[1] ^ prev[3]; state[1] = prev[0] ^ prev[1] ^ prev[2]; state[2] = prev[0] ^ prev[1] << 17 ^ prev[2]; state[3] = rotl(prev[1] ^ prev[3], 45); }
まず、簡単そうな state[3] の行を見ていきます。
一番下の rotl (n ビット左回転) は、合わせて 64 ビット回転させることで簡単に元に戻せます。両辺を 64 - 45 = 19 ビット左回転させることで、以下の関係式を得ます:
rotl(state[3], 19) == prev[1] ^ prev[3] // 64 - 45 = 19
関係式の右辺を観察すると、state[0] = ... の式に同じ要素があることに気づけます。任意の x に対して x ^ x == 0 *2 が成り立つので、両式を XOR で足し合わせると:
rotl(state[3], 19) ^ state[0] == prev[0]
prev[0] を求めることができました!
さて、ここでおもむろに state[1] = ... と state[2] = ... を見ると、やはり右辺が似たような要素で構成されています。両式を XOR すると:
state[1] ^ state[2] == prev[1] ^ prev[1] << 17
この右辺が問題になります。長いので t = prev[1]; とおいて、 t ^ t << 17 から t を得る方法を模索します。一見難しそうですが、意外と簡単に戻せます。
まず、 t ^ t << 17 を 17 bit 左シフトすると ((t ^ t << 17) << 17) == (t << 17 ^ t << 34) となります。これを元の式と XOR すると、t << 17 の項が打ち消しあって 0 になるので t ^ t << 34 になります。この操作によって、シフトを 17 → 34 と大きくできました。この調子でシフトを 64 以上にできれば、64 bit の範囲から全ビットが飛び出して 0 とみなせます。
ビット列を図にするとこんな感じです。すべてを XOR することで同じ色の部分が打ち消しあい、 t すなわち prev[1] を得ることができます。

// 左辺にも同じ操作を適用します ulong t = state[1] ^ state[2]; prev[1] == t ^ t << 17 ^ t << 34 ^ t << 51
あとは XOR のパズルで消していくだけです。
一番最初の式の両辺に、既知である prev[1] を XOR すれば prev[3] が得られます。
rotl(state[3], 19) ^ prev[1] == prev[3]
そして state[2] の式の両辺に、既知である prev[0] ^ prev[1] << 17 を XOR すれば prev[2] が得られます。
state[2] ^ prev[0] ^ prev[1] << 17 == prev[2]
以上によって、 prev を全て求めることができました。
"xor-shift" 逆算について
上の解説や図では t ^ t << k の逆算で t ^ (t << k) ^ (t << 2k) ^ (t << 3k) ^ ... とシフトを k ずつ増やしていましたが、以下のように代入を挟みながらシフトの k を 2 倍にしていくことで、小さな k に対して効率的に求められます。 *3
t ^= t << k; t ^= t << (k << 1); t ^= t << (k << 2);
また、逆算手法は右論理シフト t ^ t >> k に対しても、シフト方向を変えるだけで同様に適用可能です。
では右算術シフトの場合はどうでしょうか。 次式について考えてみましょう。
long t = some_value; long u = t ^ t >> k;
この場合、どのような t, k を選択しても u の最上位ビットは 0 になります。
t が正 (最上位ビットが 0) なら t >> k の最上位ビットも 0 、t が負 (最上位ビットが 1) なら t >> k の最上位ビットも 1 になります。これを XOR すれば、正負ともに 0 になってしまいます。
そうなると、異なる t から同一の u が得られるので、 u から t の値を確実に求めることができず、逆算はできなくなってしまいます。
ただし算術シフトが絡むとダメなのかといえばそうではなく、例えば t << k ^ t >> a は特定の k, a のペアで逆算可能になります。
shioi128 で使用されている t << 2 ^ t >> 19 などが該当します。
どのようにして逆算するかは、自分の目で確かめてみてください。 *4
PCG / 線形合同法を巻き戻す
さて次は PCG32 を巻き戻してみましょう。 ここでは出力関数を無視するので、結局のところ線形合同法と同じになります。
// ulong state = ..., ulong incr = ... | 1; public void Next() { state = state * 6364136223846793005 + incr; }
例によって結果を先に書くと、 Prev() はこのようになります。
public void Prev() { state = (state - incr) * 13877824140714322085; }
加算 (incr) のほうは移項するだけなので分かりやすいとして、乗算のほうの定数はどこから来たのでしょうか。
実は、ulong では *5 6364136223846793005 * 13877824140714322085 == 1 となります。したがって (state * 6364136223846793005) * 13877824140714322085 == state となり、逆算できます。
では肝心の定数の求め方はというと、以下の MultiplicativeInverse() メソッドによって求めることができます。任意の奇数に対して上記の性質を満たす値を計算できます。 *6
public static ulong MultiplicativeInverse(ulong x) { if ((x & 1) == 0) throw new ArgumentException("x must be odd"); ulong y = x; y = y * (2 - y * x); y = y * (2 - y * x); y = y * (2 - y * x); y = y * (2 - y * x); y = y * (2 - y * x); return y; }
メソッド内部の不思議な計算は ニュートン法 に基づいています。 時間と体力が厳しかったので解説はリンク先を参照してください。
おわりに
ここでは乱数を巻き戻す手法について紹介しました。 あまり使いどころはないかもしれませんが、実際ひとつ前の記事ではこれを調査に使っていたりします。
また、計算手法自体は出力関数の逆算にも用いることができます。例えば、Mersenne Twister の tempering (出力関数) を逆に進めて内部状態を復元するときに使えたりもします。
あえて xoshiro をチョイスしたのは、 Xorshift など有名なもの・実用されているものは先行研究が充実していて盛大に被ったためです。 それらの逆算に興味がある方は以下の記事が大変参考になります。
UnityEngine.Random の実装と性質
はじめに
Unity では、組み込みの擬似乱数生成器として UnityEngine.Random が用意されています。
この記事では、その実装や特徴について追っていきます。
※本記事の内容は Unity 2020.1.3f1 の Windows Editor にて確認したものです。
内部実装
UnityEngine.Random の遷移関数は Xorshift アルゴリズムで実装されています。
Xorshift には変種が色々ありますが、一番メジャーな実装 (Wikipedia の xor128 と同じもの) を使用しています。
// uint[] State = new uint[4] { ... }; public uint Next() { uint t = State[0] ^ State[0] << 11; State[0] = State[1]; State[1] = State[2]; State[2] = State[3]; return State[3] = State[3] ^ State[3] >> 19 ^ t ^ t >> 8; }
内部状態
内部状態は UnityEngine.Random.State 構造体 として保持されており、 state プロパティ 経由で取得・設定できます。
この構造体の中身は { int s0, s1, s2, s3; } のようになっています。各メンバーはパブリックではないので直接編集するにはリフレクションを使う必要があります。加えて、 uint ではないため注意が必要です。
内部状態を uint[] で取得・設定するメソッドは以下のようになります。(雑)
public uint[] GetBuiltinState() { var stateObject = UnityEngine.Random.state; return stateObject.GetType().GetFields(BindingFlags.NonPublic | BindingFlags.Instance) .OrderBy(field => field.Name) .Select(field => (uint)(int)field.GetValue(stateObject)) .ToArray(); } public void SetBuiltinState(uint[] state) { var stateObject = new UnityEngine.Random.State(); stateObject.GetType().GetFields(BindingFlags.NonPublic | BindingFlags.Instance) .OrderBy(field => field.Name) .Select((field, i) => { field.SetValue(stateObject, (int)state[i]); return 0; }) .ToArray(); UnityEngine.Random.state = stateObject; }
初期化
明示的に初期化するときに使う InitState メソッド の実装を調べてみましょう。
試しに公式サンプルにあった InitState(42) を呼び出すと、以下の内部状態が得られました。
0x0000002A, 0xB93C8A93, 0x49105700, 0xF3015301
[0] はそのまま引数の値 (42) のようです。後続はランダムなようですが、最下位ビットが 0, 1, 0, 1 となっており、なんとなく線形合同法の雰囲気があります。
実際にパラメータの逆算を試してみると、同じ数列を生成する線形合同法のパラメータを得ることができました。 *1
再現コードを以下に示します。
// uint State[4] として public void InitState(uint seed) { for (int i = 0; i < 4; i++) { State[i] = seed; seed = seed * 1812433253 + 1; } }
なお、ビルドしたアプリの起動時・エディタ起動時の初期状態は、InitState() 以外の方法で計算されているようです。
初期状態から 1000000 回前の状態まで遡ってみましたが *2 、どれも線形合同法の関係式を満たしませんでした。
ちなみにエディタ上では、内部状態はプレイをまたいで保持されていそうでした。
プレイ → InitState() → プレイ終了 → プレイ、とすると、前回設定したシード近辺の値が得られました。*3
エディタをいったん終了して再起動すると何らかの初期値が設定されます。
もちろんビルドしたアプリでは、何らかの方法できちんと毎回違うシードが設定されているようです。
出力
一様乱数を求める Random.value と Random.Range の実装を調べてみます。
出力を調べたところ、概ね以下の値を返すことが分かりました。
// public uint Next() がある前提で // returns [0, 1] public float value => (Next() & 0x7fffffu) / 8388607.0f; // returns [min, max) public int Range(int min, int max) => min + (int)(Next() % (uint)(max - min)); // returns [min, max]. note: 近似値を返します public float Range(float min, float max) { float t = value; // [0, 1] return t * min + (1 - t) * max; }
概ね、としたのは float Range の出力について、計算誤差?で微妙に最下位桁付近が合わない場合があるためです。上に挙げた式では正解率 70% 程度でした。もし正しい式をご存知の方がいらっしゃいましたら教えていただけると嬉しいです…
value の定数はどちらも値としては同じ 8388607 、言い換えれば です。したがって、
value の出力は概ね 23bit 精度で行われていることになります。
注記すべき点としては、value 及び float Range の出力は max を含みます。
他の言語やシステムで一般的な max を含まない出力を受け付ける前提のアルゴリズムをそのまま使用した場合 (例えば Math.Log(1 - Random.value) など)、-∞ などの予期しない値を返す可能性があるため注意が必要です。 と低確率ではありますが…
また面白い点として、int Range では Next() が大きくなるほど出力が大きくなるのに対し、 float Range では Next() が大きくなるほど出力が小さくなるようになっています。
t と 1 - t は交換しても分布が変わらないためでしょうか…?
float Range の実装が、よりシンプルである min + value * (max - min) ではない理由としては、計算誤差が上記の実装よりも大きくなるから、と推測しています。この辺りは 英語版 Wikipedia の「線形補完」の記事 に情報があります。
ちなみに、ColorHSV など一部のメソッドの実装は、UnityCsReference から確認できます。
遊んでみる
さて、内部実装が分かれば、性質を利用していろいろと遊ぶことができます。
すべて 0 の state を入れて Random を壊す
Random.state = new Random.State(); とすることで、以降 Next() から出力される乱数はすべて 0 になります。
私の環境では、それぞれ以下の数値だけを出力するようになりました。
value = 0 insideUnitCircle = (1, 0) insideUnitSphere = (0, 0, 0) onUnitSphere = (0, 0, 1) rotation = (0.5, 0.5, 0.5, 0.5) (-> euler 0, 90, 90) rotationUniform = (0, 0, 0, 0) (-> euler 0, 0, 0) ColorHSV() = (0, 0, 0, 1) (-> Black) Range(2, 12) = 2 Range(2f, 12f) = 12f
なお、前述したように内部状態はエディタを閉じるまで維持されるため、プレイを終了してもこの状態は残ります。大変邪悪ですのでよいこは真似しないでください。
解除したい場合は InitState() を適当な数値で呼び出してください。
出力から内部状態を復元する
いわゆる乱数調整というやつです。全ての内部状態が計算できれば、将来(あるいは過去)の乱数列を予測・取得することができます。
ベースは Xorshift ですから、出力から生のビット (内部状態がそのまま露出しているビット) が得られれば行列計算で内部状態復元が可能です。 行列計算については汎用的なものなので詳細は別の記事に譲るとして、Unity の出力関数から生のビットを得る方法について検討します。
value 経由
ではない数で割っているので、直接ビットを抽出することはできません。とはいえ
8388607.0 を掛ければほとんどの上位ビットは復元できるはずです。
23 bit のうち上位 16 bit だけを使って 8 個の出力を観測する、のが無難でしょうか。
// value の出力から State[3] & 0x007fff80 の情報を得ます public static uint ReverseValue(float value) => ((uint)(value * 8388607.0) & 0x7fff80);
不安定な下位ビットも取得したい場合は、& の定数を 0x7fffff としてください。
最も、乱数は大抵 [0, 1] のままではなく特定の範囲に加工して使うので、プレイヤーが value の値を直接観測できるかというと難しいとは思いますが…
int Range() 経由
max - min が偶数ならビットを抽出できます。 なら n ビット全部使えるのでなおよいです。
実用上は最も観測しやすいものかと思います。
// Range(int min, int max) の出力から State[3] の下位 n bit の情報を得ます。 // n == tzcnt(max - min) public static uint ReverseIntRange(int value, int min, int max) => (uint)(value - min) & ((1u << tzcnt((uint)(max - min))) - 1);
ややこしいことをしているように見えますが、要するに max - min の下位ビットが 0 になっているところだけ取り出すイメージです。例えば min = 0, max = pow(2, n) なら単に n ビットを取り出せばよいです。
なお、tzcnt は最下位から連続する 0 ビットの個数を返す関数とします。 System.Numerics.BitOperations.TrailingZeroCount() と等価です(が、このメソッドは Unity から簡単に参照できないようです…)。
float Range() 経由
基本的には value と同様ですが、ただでさえ近似値のところに計算を重ねるため、誤差が大きくなりそうです。
値域を [min, max] から [0, 1] に変換したうえで、value と同じ逆算を行う例を示します。
// Range(float min, float max) の出力から State[3] & 0x007fff80 の情報を得ます // ReverseValue は上述 public static uint ReverseFloatRange(float value, float min, float max) => ReverseValue((max - value) / (max - min));
ランダムな min, max に対してこのメソッドを試した限りでは、上位 16 bit を得ようとした場合の正解率は 1 回あたり 99 % 程度でした。完全復元には 128 bit 分の情報量、つまり連続 8 回の成功が必要となるので、全体としての成功率は概ね 92 % 程度でしょうか。
計算誤差の大きさに依存するので、max と value がほぼ等しい場合などでは成功率が落ちそうではあります。
おわりに
この記事では、 Unity 組み込みの擬似乱数生成器 UnityEngine.Random の実装と性質について調べました。
好きに書いた結果散らかってしまいましたが、思っていた以上に発見があり楽しかったです。
誤り・追加情報等あればご指摘いただけると助かります。
*1:計算方法については別の記事に書ければと思います
*2:Xorshift は状態を過去の方向に進めることも可能です。こちらの記事に理論と文献リンクがあります
*3:終了時の状態から 1-3 個程度進んでいる場合があります。