詳説 Ziggurat 法 ～ 正規分布・指数分布乱数の高速生成

はじめに

正規分布 や 指数分布 に従う擬似乱数を生成する際、 Ziggurat 法 を用いると高速に生成することができます。
本稿では、この Ziggurat 法の仕組みや実装について、できる限り詳しく解説していきたいと思います。

Ziggurat 法以外の手法について

早速脱線しますが、 Ziggurat 法以外にも正規分布・指数分布に従う乱数を生成する方法があります。
これらは実装が簡単であり、お世話になった方も多いかと思います。参考として挙げていきましょう。

なお、通常の System.Random では機能に不足があるので、以下のクラスを継承する擬似乱数生成器があるものとします。

public abstract class RandomBase  
{  
    /// <summary>  
    /// 64bit; [0, 2^64) の擬似乱数を生成   
    /// </summary>  
    public abstract ulong Next();  
}

Box-Muller 法

Box-Muller 法 は、正規分布に従う乱数を 2 つ生成します。
C# では、以下のように実装します。

public static (double x, double y) BoxMuller<TRng>(TRng rng)  
    where TRng : notnull, RandomBase  
{  
    // [0, 1)  
    double u0 = (rng.Next() >> 11) * (1.0 / (1ul << 53));  
    double u1 = (rng.Next() >> 11) * (1.0 / (1ul << 53));  
  
    double r = Math.Sqrt(-2 * Math.Log(1 - u0));  
    (double sin, double cos) = Math.SinCos(u1 * (Math.PI * 2));  
  
    return (r * cos, r * sin);  
}

念のため補足しておくと、 (rng.Next() >> 11) * (1.0 / (1ul << 53)) は ulong 型の乱数 [0, 2^{64}) から double 型の乱数 [0, 1) に変換するコードです。 double 型の精度は 53 bit のためこのようになっています。

Box-Muller 法は乱数の消費個数が固定なので (2 回の Next() から必ず 2 個得られる) 、乱数のストリームにフィルタをかける感じで使うなど、特定のシチュエーションでは便利です。

また余談ですが、 Wikipedia に載っている SVG が分かりやすくて素晴らしいので、一度触ってみることをおすすめします。

Polar 法

Polar 法 も、正規分布に従う乱数を 2 つ生成します。

public static (double x, double y) PolarMethod<TRng>(TRng rng)  
    where TRng : notnull, RandomBase  
{  
    double x, y, s;  
    do  
    {  
        // [-1, 1)  
        x = ((long)rng.Next() >> 10) * (1.0 / (1ul << 53));  
        y = ((long)rng.Next() >> 10) * (1.0 / (1ul << 53));  
  
        s = x * x + y * y;  
    } while (s >= 1 || s == 0);  
  
    double r = Math.Sqrt(-2 * Math.Log(s) / s);  
  
    return (x * r, y * r);  
}

さらに念のため、 ((long)rng.Next() >> 10) * (1.0 / (1ul << 53)) は double 型の [-1, 1) に変換するコードです。算術右シフトを活用して符号を設定しています。

Polar 法は乱数の消費個数がランダムです。
しかし、Box-Muller 法と比べると SinCos が不要なため、 一般に Polar 法 のほうが速くなります。

逆関数法 (指数分布)

指数分布に従う乱数を得るには、逆関数法が一番実装が簡単だと思います。

public static double Inverse<T>(T rng)  
    where T : notnull, RandomBase  
{  
    // [0, 1)  
    double u0 = (rng.Next() >> 11) * (1.0 / (1ul << 53));  
  
    return -Math.Log(1 - u0);  
}

たったこれだけで済みます。
この式は、指数分布の累積分布関数 y = 1 - \exp(-x) の逆関数 x = -\log(1 - y) からきています。

ところで、 u0 は [0, 1) なので単に -Math.Log(u0) としてもほとんど違いはないような気もしますが、こうすると u0 == 0 の場合に ∞ を返してしまい、問題の種になるので素直に 1 - u0 としています。

Ziggurat 法

以上に挙げた手法では、 Log ・ Sqrt ・ SinCos といった数学関数を使用していました。
これらは四則演算よりは重い処理になるため、できる限り使用を回避したいところです。

Ziggurat 法では、高確率でこれらの数学関数を使用せずに正規分布・指数分布に従う乱数を生成することができます。
まずは概念から説明します。
なお、一旦正規分布を中心に説明を進めていきます。

概念

Ziggurat 法の原著論文は こちら を参照してください。 *1

Ziggurat 法は棄却採択法の一種です。
棄却採択法とは、欲しい分布自体の計算が難しい・時間がかかる場合に、より大きくて単純に計算できる分布・範囲に対してランダムに点を打ち、それが欲しい分布の範囲内なら採択・範囲外なら棄却してもう一回やる、という手順から乱数を得る手法です。

Ziggurat 法は、欲しい分布の上に面積が等しい長方形を敷き詰め、その長方形上にランダムに点を打ち、それが欲しい分布の中であれば採用する、という手法です。

これは正規分布に対して 8 レイヤーの Ziggurat を置いた例です。 8 つの赤い四角形 (最下段のみ右端へ続く "尾" を含みます) はすべて同じ面積ですので、生成が簡単な一様分布に従う乱数で選択することができます。
四角形を選んだら、さらにその内部にランダムに点を打ち、それが分布より下に (中に) なればその x 座標を採択 (return して) 、そうでなければ棄却 (やり直し)、という手順で生成します。

ざっくりした生成手順としては、

  1. どのレイヤーにするか選ぶ
  2. レイヤー内にランダムに点を打ち、長方形内部か、縁のエリアかの判定
    1. 長方形内部なら、その x 座標を返す
    2. 尾の部分なら、専用の計算をして返す
    3. 縁のエリアなら、確率密度関数の下にあるか判定
      1. 収まれば、その x 座標を返す
      2. 収まらなければ、最初からやり直す

という感じです。

ちなみに、 Ziggurat 法は対象の確率密度関数が x > 0 で単調減少であるか、 y 軸に対称であれば適用可能です。
今回挙げた正規分布や指数分布以外にも、 コーシー分布 や ラプラス分布 などにも適用できます。

実装

テーブル生成

まずは各レイヤーの座標の定数テーブルを生成する必要があります。
これは分布に対して固定なので、プログラムの最初に生成するか、なんならすべて定数として埋め込んでもよいです。

/// <summary>  
/// Ziggurat 法のテーブル生成  
/// </summary>  
/// <param name="tableSize">128 or 256</param>  
/// <param name="probabilityDensityFunction">確率密度関数</param>  
/// <param name="cumulativeDistributionFunction">累積分布関数</param>  
/// <param name="inverseProbabilityDensityFunction">確率密度関数の逆関数</param>  
/// <returns>  
/// * 各レイヤー右上角の X 座標  
/// * 各レイヤー右上角の Y 座標  
/// * 各レイヤーの (確率密度関数と重ならない四角形の面積 / 全体の面積)  
/// </returns>  
public static (double[] rectangleX, double[] rectangleY, double[] insideRectangleRatio)  
    CreateZigguratTable(int tableSize,  
    Func<double, double> probabilityDensityFunction,  
    Func<double, double> cumulativeDistributionFunction,  
    Func<double, double> inverseProbabilityDensityFunction)  
{  
    double CalculateArea(double x0)  
    {  
        return x0 * probabilityDensityFunction(x0) + cumulativeDistributionFunction(double.PositiveInfinity) - cumulativeDistributionFunction(x0);  
    }  
  
    // 一番下のレイヤーの右上角の x 座標 ref. dn  
    double x0;  
    // 1 つのレイヤーの面積 ref. vn  
    double area;  
    {  
        // 誤差関数  
        double CalculateError(double x0)  
        {  
            double area = CalculateArea(x0);  
  
            double xi = x0;  
            for (int i = 1; i < tableSize; i++)  
            {  
                xi = inverseProbabilityDensityFunction(area / xi + probabilityDensityFunction(xi));  
  
                // 計算失敗時に負になる場合がある  
                if (xi < 0)  
                    return double.NegativeInfinity;  
            }  
  
            // 面積が足りない場合などに NaN になる場合がある  
            return double.IsNaN(xi) ? double.NegativeInfinity : xi;  
        }  
  
        // 探索を開始する最小値/最大値 (ヒューリスティック; 計算に失敗した場合は適宜変更する)  
        double left = 2;  
        double right = 10;  
  
        // 二分法で x0 を求める  
        while (true)  
        {  
            double mid = left * 0.5 + right * 0.5;  
  
            if (left == mid && mid < right)  
                mid = Math.BitIncrement(left);  
            else if (left < mid && mid == right)  
                mid = Math.BitDecrement(right);  
            if (left == mid || right == mid)  
                break;  
  
            double leftError = CalculateError(left);  
            double midError = CalculateError(mid);  
            double rightError = CalculateError(right);  
  
            if (Math.Sign(leftError) != Math.Sign(midError))  
                right = mid;  
            else if (Math.Sign(rightError) != Math.Sign(midError))  
                left = mid;  
            else  
                throw new InvalidOperationException("something wrong. should change left/right");  
        }  
  
        x0 = right;  
        area = CalculateArea(x0);  
    }  
  
  
    // 各レイヤー右上角の X 座標 ref. wn  
    var rectangleX = new double[tableSize];  
  
    // 各レイヤー右上角の Y 座標 ref. fn  
    var rectangleY = new double[tableSize];  
  
    // 各レイヤーの (確率密度関数と重ならない四角形の面積 / 全体の面積) ref. kn  
    var insideRectangleRatio = new double[tableSize];  
  
  
    // rectangleX の設定  
    // [0]: 一番下のレイヤーを長方形と見立てたときの横幅 (insideRectangleRatio[0] の設定のため)  
    // [1]: 一番下のレイヤー内の長方形の右端  
    rectangleX[0] = area / probabilityDensityFunction(x0);  
    rectangleX[1] = x0;  
    for (int i = 2; i < rectangleX.Length; i++)  
    {  
        double xi = inverseProbabilityDensityFunction(area / rectangleX[i - 1] + probabilityDensityFunction(rectangleX[i - 1]));  
        rectangleX[i] = xi;  
  
        if (xi < 0)  
            throw new InvalidOperationException("negative x; parameter may be wrong");  
    }  
  
    // rectangleY の設定  
    // [^1]: 頂点の y 座標  
    for (int i = 0; i < rectangleY.Length - 1; i++)  
    {  
        rectangleY[i] = probabilityDensityFunction(rectangleX[i + 1]);  
    }  
    rectangleY[^1] = probabilityDensityFunction(0);     // == 1;  
  
    // insideRectangleRatio の設定  
    // [^1]: 一番上のレイヤーはすべて範囲外なので 0  
    for (int i = 0; i < insideRectangleRatio.Length - 1; i++)  
    {  
        insideRectangleRatio[i] = rectangleX[i + 1] / rectangleX[i];  
    }  
    insideRectangleRatio[^1] = 0;  
  
  
    return (rectangleX, rectangleY, insideRectangleRatio);  
}

与える引数はこんな感じです。

  • tableSize : 定数テーブルのサイズ。通常 128 か 256
    • 2 冪にすることで高速に生成できるようにします。詳しくは後述
    • 一般に 256 のほうが速いですが、もちろん定数テーブルのサイズが大きくなります
  • probabilityDensityFunction : 確率密度関数
    • 正規分布なら x => Math.Exp(-x * x / 2)
      • 正規化定数 (分布全体の面積を 1 にするために掛けられている定数) の 1 / \sqrt{2 \pi} は無視してかまいません
    • 指数分布なら x => Math.Exp(-x)
  • cumulativeDistributionFunction : 累積分布関数
    • 正規分布なら Math.Sqrt(2 * Math.PI) * 0.5 * (1 + Erf(x / Math.Sqrt(2)))
      • Erf() は誤差関数 (後述)
    • 指数分布なら 1 - Math.Exp(-x)
  • inverseProbabilityDensityFunction : 確率密度関数の逆関数
    • 正規分布なら y => Math.Sqrt(-2 * Math.Log(y))
    • 指数分布なら y => -Math.Log(y)

Erf() は 誤差関数 \mathrm{erf}(x) = \frac{2}{\sqrt{\pi}}\int _ 0 ^ x \exp(-t ^ 2) dt です。
C# の Math にはないので、自前でテイラー展開して実装するか Math.NET Numerics などから使うかしてください。

public static double Erf(double real)  
{  
    if (double.IsInfinity(real))  
        return Math.Sign(real);         // ±∞ => ±1  
  
    double erf = 2 / Math.Sqrt(Math.PI);  
    double sum = 0;  
    double factorial = 1;  
    for (int i = 0; true; i++)  
    {  
        double element = (((i & 1) != 0 ? -1 : 1) * Math.Pow(real, 2 * i + 1)) /  
            (factorial * (2 * i + 1));  
  
        if (sum + element == sum)  
            break;  
  
        sum += element;  
        factorial *= i + 1;  
    }  
    return sum * erf;  
}
area と x0 の計算手法

area (各レイヤーの面積) や x0 (一番下のレイヤーの右角 x 座標) といった定数の計算手法について説明します。

tableSize が 256 のとき、面積 A は以下の関係式を満たします:

\begin{aligned} A &= x_0 \mathrm{PDF}(x_0) + \int_{x_0} ^ \infty \mathrm{PDF}(x)dx & \\ A &= x_{i-1} (\mathrm{PDF}(x_i) - \mathrm{PDF}(x_{i-1})) & (i=1, 2, ..., 254) \\ A &= x_{254} (\mathrm{PDF}(x_{255}) - \mathrm{PDF}(x_{254})) \\ &= x_{254} (\mathrm{PDF}(0) - \mathrm{PDF}(x_{254})) \end{aligned}

\mathrm{PDF}(x) は確率密度関数です。

2 番目の式を変形して、

\begin{aligned} \frac{A}{x_{i-1}} &= \mathrm{PDF}(x_i) - \mathrm{PDF}(x_{i-1}) \\ \frac{A}{x_{i-1}} + \mathrm{PDF}(x_{i-1}) &= \mathrm{PDF}(x_i) \\ \mathrm{PDF}^{-1}(\frac{A}{x_{i-1}} + \mathrm{PDF}(x_{i-1})) &= x_i \end{aligned}

とします。 \mathrm{PDF}^{-1}(x) は確率密度関数の逆関数で、 \mathrm{PDF}^{-1}(\mathrm{PDF}(x) ) = x を満たすような関数です。
すると、 x_0 を決める → A が決まる → x_i が次々決まっていく → 最後の式

\mathrm{PDF}^{-1}(\frac{A}{x_{254}} + \mathrm{PDF}(x_{254})) = x_{255} = 0

を満たしているかを確認する、といった手順で求めることはできそうです。

問題は最初の x_0 なのですが、どうやら数学的にうまいこと解くのは難しいらしく、求根アルゴリズム (二分法や割線法など) を使って求めることになります。

幸いにして x_0 はそこまで広い範囲にはないことが予想されるので (せいぜい 2 \lt x_0 \lt 10 程度でしょう) 、今回は 二分法 を使って解きます。

二分法は、以下のような手順で f(x) = 0 となる x を計算するアルゴリズムです。

  1. 探索の最小値 left と最大値 right を決める
  2. 中点 mid を求める
  3. 符号に合わせて left か right を更新する
    1. sign(f(left)) != sign(f(mid)) なら right = mid
    2. sign(f(right)) != sign(f(mid)) なら left = mid
  4. 以上を left と right が十分に狭い範囲になるまで繰り返す
  5. left か right を目的の値として返す

area と x0 は、 tableSize に合わせて次のようになるはずです。

分布 tableSize area x0
正規分布 128 0.0099125630353356087 3.4426198558966847
正規分布 256 0.0049286732339721695 3.6541528853613281
指数分布 128 0.0079732295395533725 6.8983151166156444
指数分布 256 0.0039496598225815527 7.6971174701310288
定数テーブルの中身

CreateZigguratTable() で何が計算できるかを図で見てみましょう。
尾のあたりを拡大して見てみます:

rectangleX と rectangleY には各レイヤーの角の座標、 insideRectangleRatio にはオレンジ色のエリア (確率密度関数と交わる部分を含まない面積の割合) の情報が入っています。
rectangleX[0] は図にありませんが、これには別の値、具体的にはレイヤー 0 (一番下)を長方形と見立てたときの横幅が入っています。なぜこうするのかというと、 insideRectangleRatio[0] で (レイヤー 0 の長方形部分の面積 / レイヤー 0 全体の面積) を計算するためです。

頭のあたりを拡大するとこんな感じです。
(念のため、インデックスの [^i] は最後から i 番目 (最後の要素は [^1]) を表します。)

一番上のレイヤーの insideRectangleRatio[^1] は 0 になっていることに注意してください。

分布に従う乱数の生成

さて、テーブルの生成が終わったら、本題の乱数生成に入ります。

// CreateZigguratTable で生成した定数テーブル  
private static readonly double[] ZigguratNormalX = new double[] { ... };  
private static readonly double[] ZigguratNormalY = new double[] { ... };  
private static readonly double[] ZigguratNormalInsideRectangleRatio = new double[] { ... };  
  
public static double ZigguratNormal<TRng>(TRng rng)  
    where TRng : notnull, RandomBase  
{  
    const int TableSize = 256;  
  
    while (true)  
    {  
        long u1 = (long)rng.Next();  
        // [-1, 1)  
        double u1Double = (u1 >> 10) * (1.0 / (1ul << 53));  
        int rectangleIndex = (int)(u1 & (TableSize - 1));  
  
        // 確率密度関数の範囲内にある四角形なら、そのまま返す  
        if (Math.Abs(u1Double) < ZigguratNormalInsideRectangleRatio[rectangleIndex])  
            return u1Double * ZigguratNormalX[rectangleIndex];  
  
        if (rectangleIndex == 0)  
        {  
            // 一番下のレイヤーの尾の部分  
            double s, t;  
            double x0 = ZigguratNormalX[1];  
            do  
            {  
                s = -Math.Log(1 - (rng.Next() >> 11) * (1.0 / (1ul << 53))) / x0;  
                t = -Math.Log(1 - (rng.Next() >> 11) * (1.0 / (1ul << 53)));  
            } while (s * s > t + t);  
  
            return (x0 + s) * (u1 < 0 ? -1 : 1);  
        }  
        else  
        {  
            // それ以外の端の部分  
            double x = u1Double * ZigguratNormalX[rectangleIndex];  
            double y = (rng.Next() >> 11) * (1.0 / (1ul << 53));  
  
            if (ZigguratNormalY[rectangleIndex - 1] + y * (ZigguratNormalY[rectangleIndex] - ZigguratNormalY[rectangleIndex - 1]) <= Math.Exp(-0.5 * x * x))  
                return x;  
        }  
    }  
}

順を追って説明していきましょう。

テーブル選択・四角形の中にあるか判定
long u1 = (long)rng.Next();  
// [-1, 1)  
double u1Double = (u1 >> 10) * (1.0 / (1ul << 53));  
int rectangleIndex = (int)(u1 & (TableSize - 1));

まずは一様分布に従う乱数を生成して、 u1Double を -1.0 <= u1Double < 1.0 の範囲で、どのレイヤーを選ぶかを決める rectangleIndex を 0 <= rectangleIndex < tableSize の範囲で生成します。
テーブル生成にて tableSize を 2 冪にしておいたのは、ここで rectangleIndex をビットマスクだけで生成できるようにするためです。

// 確率密度関数の範囲内にある四角形なら、そのまま返す  
if (Math.Abs(u1Double) < ZigguratNormalInsideRectangleRatio[rectangleIndex])  
    return u1Double * ZigguratNormalX[rectangleIndex];

次に、選択されたレイヤーの insideRectangleRatio[rectangleIndex] (オレンジの領域) 内に u1Double が入っているかを判定します。もし入っていればそれは確実に確率密度関数 (青線) の下にあるので、その x 座標、つまり u1Double * rectangleX[rectangleIndex] を返します。

ちなみに、正規分布で tableSize が 256 の場合は約 98.5 % の確率でここで採択されます。

そうでない場合は後続の処理に続きます。

尾の範囲外処理
// 一番下のレイヤーの尾の部分  
double s, t;  
double x0 = ZigguratNormalX[1];  
do  
{  
    // note: (rng.Next() >> 11) * (1.0 / (1ul << 53))  
    // は [0, 1) の乱数を生成する  
    s = -Math.Log(1 - (rng.Next() >> 11) * (1.0 / (1ul << 53))) / x0;  
    t = -Math.Log(1 - (rng.Next() >> 11) * (1.0 / (1ul << 53)));  
} while (s * s > t + t);  
  
return (x0 + s) * (u1 < 0 ? -1 : 1);

選ばれたのが一番下のレイヤーで、かつ範囲外だった場合は一工夫が必要です。
正規分布では、上記のコードで尾の部分の乱数を生成することができます。

……どうして?

説明していきましょう。こちらについては、文献 *2 を参考にしつつ解説します。

まず、正規分布の確率密度関数から正規化定数を除いた \exp(-x ^ 2/2) と、一番下のレイヤーの右角 (rectangleX[1]) である x_0 について、

\begin{aligned} x &\ge x_0 \\ (x-x_0)^2 &\ge 0 \\ x^2 - 2x_0 x + x_0^2 &\ge 0 \\ x^2 &\ge 2x_0 x - x_0^2 \\ -\frac{x^2}{2} &\le \frac{x_0^2}{2} - x_0 x \\ \exp(-\frac{x^2}{2}) &\le \exp(\frac{x_0 ^2}{2}-x_0 x) \end{aligned}

となるので、 \exp(x_0 ^ 2 / 2 - x_0 x) は常に正規分布の確率密度関数より大きくなります。したがって棄却採択法の関数として使えます。
(繰り返しになりますが、計算が簡単でより大きな分布を持つ関数で覆ってしまって、その内部に点を打ち、それが計算が複雑で小さい分布 (ここでは正規分布) の中にあれば OK 、というのが棄却採択法です。)

確率密度を求めるため、 [x_0, \infty) の範囲で積分すると、

\begin{aligned} & \int_{x_0}^\infty \exp(\frac{x_0^2}{2}-x_0 x) dx \\ &= \exp(\frac{x_0^2}{2}) \int_{x_0}^\infty \exp(-x_0 x) dx \\ &= \exp(\frac{x_0^2}{2}) \cdot \frac{\exp(-x_0^2)}{x_0} \\ &= \frac{\exp(-\frac{x_0^2}{2})}{x_0} \end{aligned}

になりますので、これで当初の式を割って正規化すると

\frac{\exp(x_0^2/2-x_0 x)}{\exp(-x_0^2/2)/x_0} = x_0 \exp(x_0^2 - x_0x)

を得ます。これが確率密度関数になります。
この累積分布関数は、

\begin{aligned} & \int_{x_0}^x x_0 \exp(x_0^2 - x_0 y) dy \\ &= x_0 \exp(x_0^2) \int_{x_0}^x \exp(-x_0 y) dy \\ &= x_0 \exp(x_0^2) ( (-\frac{\exp(-x_0 x)}{x_0}) - (-\frac{\exp(-x_0^2)}{x_0}) ) \\ &= 1 - \exp(x_0^2 - x_0x) \end{aligned}

となります。この逆関数を求めましょう。

\begin{aligned} s &= 1 - \exp(x_0^2 - x_0x) \\ 1-s &= \exp(x_0^2 - x_0x) \\ \log(1-s) &= x_0^2 - x_0x \\ -x_0^2+\log(1-s) &= -x_0x \\ x_0 - \frac{1}{x_0}\log(1-s) &= x \end{aligned}

注意すべきポイントとしては、 s=1 とすると \log(0)=-\infty なので x=\infty となってしまうので、そうならないように s の範囲を [0, 1) として 1-s にしています。

ここで、 [0, 1) の範囲の一様分布乱数 t を用意して、 \exp(x_0 ^ 2 / 2 - x_0 x) に 1-t を掛けた (1-t) \exp(x_0 ^ 2 / 2 - x_0 x) がもともとの \exp(-x ^ 2 / 2) を下回れば分布の中に入るので採択、そうでなければ棄却、としましょう。

\begin{aligned} (1-t) \exp(\frac{x_0^2}{2}-x_0x) &\le \exp(-\frac{x^2}{2}) \\ 1-t &\le \exp(-\frac{x^2}{2} + x_0x - \frac{x_0^2}{2}) \\ 1-t &\le \exp(-\frac{(x-x_0)^2}{2}) \\ \log(1-t) &\le -\frac{(x-x_0)^2}{2} \\ -2\log(1-t) &\ge (x-x_0)^2 \end{aligned}

先ほど求めた逆関数 x_0 - \frac{1}{x_0}\log(1-s) = x より、 x - x_0 = -\frac{1}{x_0}\log(1-s) ですから、

-2\log(1-t) \ge (-\frac{1}{x_0}\log(1-s))^2

を得ます。
さらに T = -\log(1-t), S = -\frac{1}{x_0}\log(1-s) とおけば、

\begin{aligned} 2T &\ge S^2 \\ S \times S &\le T + T \end{aligned}

ここまで来れば見覚えのある式になったのではないでしょうか?
コードをもう一度見直してみましょう。

// 一番下のレイヤーの尾の部分  
double s, t;  
double x0 = ZigguratNormalX[1];  
do  
{  
    s = -Math.Log(1 - (rng.Next() >> 11) * (1.0 / (1ul << 53))) / x0;  
    t = -Math.Log(1 - (rng.Next() >> 11) * (1.0 / (1ul << 53)));  
} while (s * s > t + t); // 棄却されたらやり直しなので、不等号が逆  
  
return (x0 + s) * (u1 < 0 ? -1 : 1);

このような処理になった理由が分かったかと思います。

また、 こちらのブログ にも別のアプローチも含めて詳しく述べられています。

また、指数分布ではこのように処理します。

// 一番下のレイヤー (尾の部分)  
double x0 = ZigguratExponentialX[1];  
return x0 + ZigguratExponential(rng);

指数分布の尾の部分の処理は、単に x_0 を足して指数分布と同じ手法を再帰的に適用するだけでよいです。
なぜかを説明します。

x_0 より右側の部分の面積は、

\begin{aligned} & \int _ {x_0} ^ {\infty} \exp(-x) dx \\ &= (-\exp(-\infty)) - (-\exp(-x_0)) \\ &= \exp(-x_0) \end{aligned}

です。次に、 x_0 以上の部分の累積分布関数を求めます。
通常時の累積分布関数の始点を x_0 にしたうえで面積で割ることで、

\begin{aligned} & \frac{1}{\exp(-x_0)} \int _ {x_0} ^ {x} \exp(-x) dx \\ &= \exp(x_0) ( (-\exp(-x)) - (-\exp(-x_0)) ) \\ &= 1 - \exp(-x + x_0) \end{aligned}

となりますので、その逆関数は、

\begin{aligned} y &= 1 - \exp(-x + x_0) \\ 1 - y &= \exp(-x + x_0) \\ \log(1-y) &= -x + x_0 \\ x_0 - \log(1-y) &= x \end{aligned}

となります。これは、通常時の累積分布関数の逆関数 x=-\log(1-y) に x_0 を足したものになります。

というわけで、 x_0 を足して指数分布に従う乱数を再帰的に生成すればよいことになります。
(再帰すると遅いので、実際はループで処理します。)

それ以外の範囲外処理

さて、尾以外の部分で範囲外となった場合は、以下のように処理していました。

// それ以外の端の部分  
double x = u1Double * ZigguratNormalX[rectangleIndex];  
double y = (rng.Next() >> 11) * (1.0 / (1ul << 53));  
  
if (ZigguratNormalY[rectangleIndex - 1] + y * (ZigguratNormalY[rectangleIndex] - ZigguratNormalY[rectangleIndex - 1]) <= Math.Exp(-0.5 * x * x))  
    return x;

位置関係を図にするとこんな感じになります。

こういう感じで座標を計算して、それが確率密度関数よりも低ければ採択、そうでなければ棄却してやり直します。

高速化ポイント

オリジナルの実装では、 insideRectangleRatio を整数型にして直接 u1 (整数乱数) と比較することで、浮動小数点数型同士ではなく整数型同士の比較にして高速化を図っているようです。

また、 rectangleX に 2^{63} などをあらかじめ掛けておくことで、 u1Double のシフト・定数との掛け算を省いて直接 u1 * rectangleX[rectangleIndex] として返す、といった手法もあります。

今回は分かりやすさを重視したため以上の手法は使っていませんが、高速化の余地はあります。

改良 Ziggurat 法

Ziggurat 法には改良されたバージョンがあります。 *3
改良 Ziggurat 法は Java の nextGaussian() ・ nextExponential() の実装でも 使われています。

こちらの紹介もしていきたいと思います。
なんなら今までが前置きでここから本題です。

概念 ～ 改良されたポイント

Ziggurat の配置について

改良 Ziggurat 法の Ziggurat を見てみましょう。

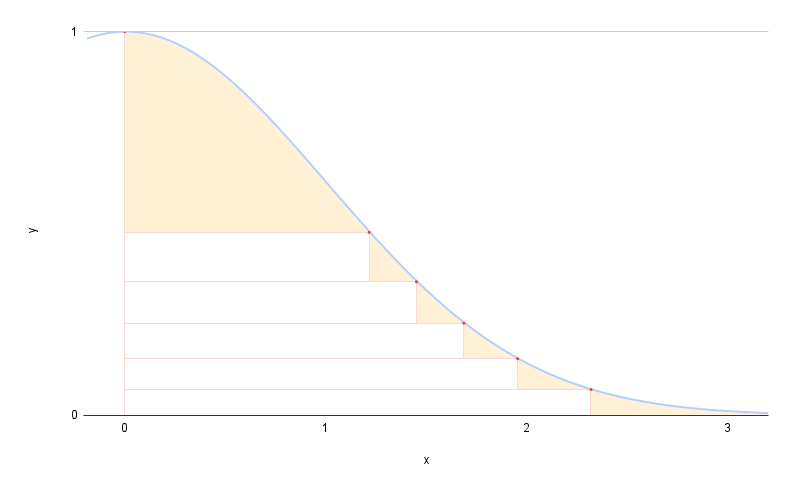
これは、正規分布に対して 8 レイヤーの Ziggurat を置いた例です。
……はい。 8 レイヤーです。でも 5 レイヤーしかありませんし、確率密度関数からはみ出していません。
これでは破綻しているのでは? と思われるかもしれませんので、説明を続けます。

残りの 3 レイヤーはどこにあるのかというと、四角形の外と確率密度関数に挟まれた端の (オレンジ色の) 部分です。
実は端の部分の面積をすべて足すと、ちょうどレイヤー 3 枚分になります。
これによって、「同じ面積のレイヤーをランダムに (一様分布の乱数で) 選択する」機能を維持することができます。
また、それ以外の四角形のレイヤーが選択された場合に、端の処理をせずに即採択することができます。厄介だった端の処理を 3 枚分に押し込めたイメージです。
正規分布では、全体の約 98.8 % が四角形のレイヤーで採択されます。よく通るパスで端の処理を省略できるため、高速化につながります。

それでは実際に端の 3 枚分が選択された場合はどのようにして生成するのかというと、

  1. 各レイヤーの端の部分の面積を重みにした重み付き抽選を行い、レイヤーインデックス j を得る
  2. Ziggurat 法と同様に、レイヤー j における端の部分の処理を行う
    1. レイヤー 0 (一番下) の場合は、尾から生成する処理を行う
    2. それ以外のレイヤーの場合は、確率密度関数より下になるかを判定して棄却/採択する

という感じで、レイヤーを再抽選したあとは Ziggurat 法で端を引いた時と似たような処理になります。

最初に重み付き抽選を行うのは、もちろん各レイヤーの端の部分の面積がそれぞれ異なるからです。
先ほどの図を見ていただければわかる通り、一番上のレイヤーの端は巨大で、その下のレイヤーの端と比べると一目瞭然でしょう。
そのため、その面積に従って重み付き抽選をする必要があります。

重み付き抽選を安直にやってしまうと時間がかかるので、 Walker's Alias method を利用します。

Walker's Alias method

Walker's Alias method は、事前にテーブル生成をすることで重み付き抽選を高速に行うアルゴリズムです。 *4

通常、重み付き抽選には O(n) 、重み順にソートして二分探索するなどしても O(\log(n)) はかかりますが、 Alias method を利用すると抽選は O(1) で行うことができます。驚きの速さです。

その分事前に O(n) かかるテーブル生成をする必要があるため、重みを場合によって変えたり、重みテーブルを 1 回しか使わなかったりする場合では安直な方法より遅くなりがちです。重みを変えずに何度も抽選する場合に有効なアルゴリズムであるといえます。
今回適用したい確率分布は絶対に重みが変わらないため事前にテーブル生成を済ませておくことができ、まさにおあつらえ向きな手法です。

実例を挙げると、前述した各レイヤーの端部分の面積はこのようになっています。
一番上のレイヤーが重い (大きい) ことがよくわかります。

これを、

  • 全てのレイヤーが同じ重さになるように、 8 つのレイヤーに切り分ける
  • 1 つのレイヤーに 2 種類まで入れる
  • 2 種類のうち 1 つは元々あったもの

というルールでいい感じに分割すると、以下のようになります。

端に振ってある数字が元々のレイヤーのインデックス (一番下が 0 番目) です。
大きかった 5 番目 (一番上) がまんべんなく振られていますね。
ちなみに、上 3 つの左側には重さ 0 の青いほうがあるものとします。

この振り分けが終わると、以下の手順で重み付き抽選をすることができます。

  1. 乱数を生成し、レイヤーをランダムに選ぶ。
  2. 0 ～ 1 の乱数を生成し、閾値未満なら元々のインデックス (左の青いほう) 、閾値以上なら 2 番目のインデックス (右の赤いほう) を返す。

これはテーブルを毎回走査する必要がなく、乱数消費も 2 個固定です。したがって O(1) で重み付き抽選が実現されます。

このテーブルが持つべき情報は、「左側の重み」「右側のインデックス」です。
右側の重みは (1 - 左側の重み) になりますし、左側のインデックスはそのレイヤーのインデックスと同じにしてあるためです。

なお、詳しいテーブル作成手法などについては、 Wikipedia や こちらの記事 が参考になります。

端の部分の最適化

さらに最適化を進めます。

端の部分の判定を行うとき、今までは単に「確率密度関数より下に行くか?」を見ていましたが、ここにも最適化の余地があります。

端の部分は大体三角形をしています。中でも、「ふくらんだ三角形」「へこんだ三角形」「ふくらみとへこみのある三角形」に分類することができます。

ふくらんだ三角形

一番上のレイヤーを例に挙げて説明しましょう。

まず、この四角形の領域に斜線を引いて三角形を作りましょう。
すると、ふくらんだ三角形の場合、左下のオレンジの三角形の部分は常に青線の確率密度関数より下になることがわかります。
したがって、ランダムに打った点がオレンジの領域に入った場合は、確率密度関数の計算を省略して採択することができます。
確率密度関数の計算では Math.Exp(-0.5 * x * x) や Math.Exp(-x) など相対的に重い指数関数を使いますので、これを省略できるとスピードアップにつながります。

また、一番ふくらんでいるところに接するように、同じ傾きの線を引きます。
すると、右上の水色の三角形の部分は常に青線の確率密度関数より上になり、同様に確率密度関数の計算を省略して棄却することができます。

なお、オレンジと水色の三角形に挟まれた部分はどうしようもないので、今までと同様に確率密度関数の計算を行ってそれより下かを判定します。

へこんだ三角形

下から二番目のレイヤーを例に挙げて説明しましょう。

上と同様に、一番へこんでいるところに接するように同じ傾きの線を引くと、左下のオレンジ色の部分は必ず採択される領域になります。

また、左上の部分はそのままだと必ず棄却される領域になりますが、もったいないので 180°回転させる (または上下左右を反転させる) ことで再抽選を行います。
再抽選でも同様に、左下の緑色の部分は必ず採択、残った水色の部分は諦めて確率密度関数との計算を行うようにします。

なお、指数分布ではふくらみはないので、全ての領域がへこんだ三角形になります。

ふくらみとへこみのある三角形

ふくらみとへこみの中間地点がこれにあたります。
ここでも同様に、

  • 一番へこんでいるところに接するように同じ傾きの線を引き、それより下は採択
  • 一番ふくらんでいるところに接するように同じ傾きの線を引き、それより上は棄却
  • その中間では通常通り、確率密度関数との判定

とします。

尾の生成の最適化

さて、一番下のレイヤーの尾の部分についても考えてみましょう。

以前は尾の部分の生成ではこういう感じのコードになっていました。

// 一番下のレイヤーの尾の部分  
double s, t;  
double x0 = ZigguratNormalX[1];  
do  
{  
    s = -Math.Log(1 - (rng.Next() >> 11) * (1.0 / (1ul << 53))) / x0;  
    t = -Math.Log(1 - (rng.Next() >> 11) * (1.0 / (1ul << 53)));  
} while (s * s > t + t);  
  
return (x0 + s) * (u1 < 0 ? -1 : 1);

ここで、 -Math.Log(...) の部分に着目してみましょう。
これは、冒頭で述べた「逆関数法による指数分布に従う乱数生成」と同じになります。
したがって、 (改良) Ziggurat 法による生成のほうが速いのであれば、それに置き換えることができます。

// 最下層レイヤー: 尾から生成する  
double x0 = ModifiedZigguratNormal128X[0] * (1ul << 63);  
double s, t;  
do  
{  
    s = ModifiedZigguratExponential(rng) / x0;  
    t = ModifiedZigguratExponential(rng);  
} while (s * s > t + t);  
return (x0 + s) * (u1 < 0 ? -1 : 1);

実装

以上を踏まえて、実装に移っていきましょう。
まずは定数テーブル生成からやります。

定数テーブル生成

改良 Ziggurat 法においては、面積 (A) は単純に (全域の面積 / tableSize) で求めることができます。はみ出す部分がないのでここの計算は楽です。

今回の正規分布での関係式は、

\begin{aligned} A &= x_0 \mathrm{PDF}(x_0) \\ A &= x_i (\mathrm{PDF}(x_i) - \mathrm{PDF}(x_{i-1}) ) & (i=1, 2, ..., 252) \\ 3A &= \int_{0}^{\infty} \mathrm{PDF}(x) dx - \sum_{i=0}^{252} x_i \mathrm{PDF(x_i)} \\ &= \mathrm{CDF}(\infty) - \mathrm{CDF}(0) - 253A \\ 256A &= \mathrm{CDF}(\infty) - \mathrm{CDF}(0) \\ \end{aligned}

となります。なお、 \mathrm{CDF} は累積分布関数です。
まずは最後の式から A を求めることができます。
そして 2 番目の式から、

\begin{aligned} A &= x_i (\mathrm{PDF}(x_i) - \mathrm{PDF}(x_{i-1}) ) \\ A / x_i &= \mathrm{PDF}(x_i) - \mathrm{PDF}(x_{i-1}) \\ \mathrm{PDF}(x_i) - A / x_i &= \mathrm{PDF}(x_{i-1}) \\ \mathrm{PDF}^{-1}(\mathrm{PDF}(x_i) - A / x_i) &= x_{i-1} \end{aligned}

となるので、 x _ {i} から x _ {i-1} を求めることができます。
したがって、 x_{252} (上から 2 番目のレイヤーの四角形右端) を決める → x_i が決まっていく → x_0 が決まる → 最初の式 A = x_0 \mathrm{PDF}(x_0) を満たすかを確認する、といった手順で進められます。

Ziggurat 法とは決定の順序が異なり、上から順 (インデックスが大きな順) なことに注意してください。
また、指数分布の場合は端の面積が 3 レイヤーだと足りず 4 レイヤー分になるので、 3 (252) を 4 (251) に読み替えてください。

/// <summary>  
/// 改良 Ziggurat 法のテーブル生成  
/// </summary>  
/// <param name="tableSize">128 or 256</param>  
/// <param name="iMax">正規分布は <paramref name="tableSize"/>-3, 指数分布は <paramref name="tableSize"/>-4 </param>  
/// <param name="isSymmetric">正規分布は true, 指数分布は false</param>  
/// <param name="probabilityDensityFunction">確率密度関数</param>  
/// <param name="cumulativeDistributionFunction">累積分布関数</param>  
/// <param name="inversePdf">確率密度関数の逆関数</param>  
/// <param name="derivativePdf">確率密度関数の傾き (微分)</param>  
/// <returns>  
/// * X に係数 2^-n を掛けたもの; n=63(正規分布) or 64(指数分布)  
/// * Y に係数 2^-n を掛けたもの  
/// * 上位 56 bit が 1 つめの重み, 下位 8 bit が 2 つめのインデックスである Walker's Alias method のテーブル  
/// * 変曲点 (確率密度関数のへこみとふくらみの境界) のレイヤーのインデックス  
/// * 最大のふくらみの比  
/// * 最大のへこみの比  
/// </returns>  
public static (double[] x, double[] y, ulong[] aliasBox, int inflectionIndex, ulong maxConvexRate, ulong maxConcaveRate)  
    CreateModifiedZigguratTable(int tableSize, int iMax, bool isSymmetric,  
    Func<double, double> probabilityDensityFunction,  
    Func<double, double> cumulativeDistributionFunction,  
    Func<double, double> inversePdf,  
    Func<double, double> derivativePdf)  
{  
    // 1 レイヤーの面積  
    var area = (cumulativeDistributionFunction(double.PositiveInfinity) - cumulativeDistributionFunction(0)) / tableSize;  
  
    // 二分法  
    static double Bisection(Func<double, double> errorFunction, double initialLeft, double initialRight)  
    {  
        double left = initialLeft;  
        double right = initialRight;  
  
        while (true)  
        {  
            double mid = left * 0.5 + right * 0.5;  
  
            if (left == mid && mid < right)  
                mid = Math.BitIncrement(left);  
            else if (left < mid && mid == right)  
                mid = Math.BitDecrement(right);  
            if (left == mid || right == mid)  
                break;  
  
            double leftError = errorFunction(left);  
            double midError = errorFunction(mid);  
            double rightError = errorFunction(right);  
  
            if (Math.Sign(leftError) != Math.Sign(midError))  
                right = mid;  
            else if (Math.Sign(rightError) != Math.Sign(midError))  
                left = mid;  
            else  
                throw new InvalidOperationException("something wrong. should change left/right");  
        }  
  
        return left;  
    }  
  
  
    // xtop (x[iMax]) を二分法で求める  
    double xtop;  
    {  
        // 探索の最小/最大値。(ヒューリスティック; 動かないときは適宜変更する)  
        double xtopLeft = 0.01;  
        double xtopRight = 0.5 * (isSymmetric ? 1.0 : 0.4);  
  
        // 探索の誤差関数。最後のレイヤーの x 座標まで計算可能なら負の、不可能なら正の値を返す  
        double CalculateError(double xtop)  
        {  
            for (int i = iMax - 1; i >= 0; i--)  
            {  
                xtop = inversePdf(probabilityDensityFunction(xtop) - area / xtop);  
  
                if (double.IsNaN(xtop))  
                    return i + 1;  
            }  
            return -xtop;  
        }  
  
        xtop = Bisection(CalculateError, xtopLeft, xtopRight);  
    }  
  
  
    // x, y の設定  
    var x = new double[iMax + 1];  
    var y = new double[iMax + 1];  
  
    x[^1] = 0;  
    y[^1] = probabilityDensityFunction(0);  
    x[^2] = xtop;  
    y[^2] = probabilityDensityFunction(xtop);  
    for (int i = x.Length - 3; i >= 0; i--)  
    {  
        x[i] = inversePdf(probabilityDensityFunction(x[i + 1]) - area / x[i + 1]);  
        y[i] = probabilityDensityFunction(x[i]);  
  
        // verification  
        double actual = x[i + 1] * (y[i + 1] - y[i]);  
        if (Math.Abs(actual - area) > 1.0 / (1ul << 52) || double.IsNaN(actual))  
            throw new InvalidOperationException("area mismatch");  
    }  
  
  
    // 各レイヤー端の面積の計算  
    var edgeArea = new double[iMax + 1];  
    edgeArea[0] = cumulativeDistributionFunction(double.PositiveInfinity) - cumulativeDistributionFunction(x[0]);  
    for (int i = 1; i < edgeArea.Length; i++)  
    {  
        edgeArea[i] = (cumulativeDistributionFunction(x[i - 1]) - cumulativeDistributionFunction(x[i]))  
            - y[i - 1] * (x[i - 1] - x[i]);  
    }  
    // verification  
    {  
        double actual = edgeArea.Sum();  
        if (Math.Abs(actual - area * (tableSize - iMax)) > 1.0 / (1ul << 50))  
            throw new InvalidOperationException("edgeArea mismatch");  
    }  
  
  
    // Walker's Alias method によるテーブル作成  
    var firstWeights = new double[tableSize];  
    var secondIndexes = Enumerable.Range(0, tableSize).ToArray();  
    double edgeAverage = (tableSize - iMax) * area / tableSize;  
    {  
  
        for (int i = 0; i < edgeArea.Length; i++)  
            firstWeights[i] = edgeArea[i];  
  
        // 小さい順に並べ替える  
        var sorted = Enumerable.Range(0, tableSize).ToArray();  
        Array.Sort(sorted, Comparer<int>.Create((a, b) => firstWeights[a].CompareTo(firstWeights[b])));  
  
        // 最大の要素から最小の要素に分配していく  
        int small = 0;  
        int large = firstWeights.Length - 1;  
        while (small < large)  
        {  
            secondIndexes[sorted[small]] = sorted[large];  
  
            firstWeights[sorted[large]] -= edgeAverage - firstWeights[sorted[small]];  
  
            switch (firstWeights[sorted[large]].CompareTo(edgeAverage))  
            {  
                case > 0:  
                    small++;  
                    break;  
                case 0:  
                    small++;  
                    firstWeights[sorted[large]] = edgeAverage;  
                    secondIndexes[sorted[large]] = sorted[large];  
                    large--;  
                    break;  
                case < 0:  
                    (sorted[small], sorted[large]) = (sorted[large], sorted[small]);  
                    large--;  
                    break;  
            }  
        }  
  
    }  
    // firstWeights 正規化と検証  
    for (int i = 0; i < firstWeights.Length; i++)  
    {  
        if (firstWeights[i] - edgeAverage > 1.0 / (1ul << 52))  
            throw new InvalidOperationException("weight mismatch");  
  
        firstWeights[i] /= edgeAverage;  
    }  
  
  
    // 変曲点・ふくらみ/へこみの最大値の探索  
    int inflectionIndex = tableSize;  
    double maxConvexRatio = 0;  
    double maxConcaveRatio = 0;  
    for (int i = 1; i < x.Length; i++)  
    {  
        // > 0 ならふくらみ(convex), < 0 ならへこみ(concave)  
        double GradientDifference(double t)  
        {  
            double pdfGradient = derivativePdf(t);  
            double lineGradient = (y[i] - y[i - 1]) / (x[i] - x[i - 1]);  
            return pdfGradient - lineGradient;  
        }  
  
        double maxGradientPoint = Bisection(GradientDifference, x[i], x[i - 1]);  
  
  
        if (inflectionIndex == tableSize && GradientDifference(maxGradientPoint) > 0)  
        {  
            inflectionIndex = i;  
        }  
        {  
            double lineGradient = (y[i] - y[i - 1]) / (x[i] - x[i - 1]);  
            double diff = probabilityDensityFunction(maxGradientPoint) -  
                (lineGradient * maxGradientPoint + y[i] - lineGradient * x[i]);  
            double ratio = diff / (y[i] - y[i - 1]);  
  
            if (i < inflectionIndex)  
                maxConcaveRatio = Math.Max(-ratio, maxConcaveRatio);  
            else  
                maxConvexRatio = Math.Max(ratio, maxConvexRatio);  
        }  
    }  
  
  
    // x, y のスケール  
    for (int i = 0; i < x.Length; i++)  
    {  
        x[i] *= (isSymmetric ? 1.0 : 0.5) / (1ul << 63);  
        y[i] *= (isSymmetric ? 1.0 : 0.5) / (1ul << 63);  
    }  
  
    // Walker's Alias method のテーブルを一つにまとめる  
    var aliasBox = new ulong[tableSize];  
    for (int i = 0; i < aliasBox.Length; i++)  
    {  
        ulong ulongWeight = (ulong)(firstWeights[i] * (2.0 * (1ul << 63)));  
  
        // verification  
        if ((ulongWeight & ((ulong)tableSize - 1)) != 0)  
            throw new InvalidOperationException("weight may lose precision");  
  
        aliasBox[i] = ulongWeight ^ (ulong)secondIndexes[i];  
    }  
  
    return (x, y, aliasBox, inflectionIndex, (ulong)(maxConvexRatio * (2.0 * (1ul << 63))), (ulong)(maxConcaveRatio * (2.0 * (1ul << 63))));  
}

以下、要所の説明をしていきます。

ふくらみ・へこみの計算

ふくらみ・へこみの計算では、「確率密度関数の傾き」が「四角形の左上と右下を結ぶ直線の傾き」が同じになる (または近づく) ポイントを探します。そこがふくらみ/へこみ (確率密度関数と直線との高さの差) が最大化されるポイントになります。
この図をもう一度見ていただくとわかりやすいかと思います。

ここで、ふくらみ・へこみは、四角形の高さとの割合として記録しておき、かつ全レイヤー中の最大値だけを取っておくようにします。これによって定数テーブルを増やさずに済みます。
原著論文曰く、これをテーブル化しても速度の向上につながらなかったそうです。 (Appendices D の 2 を参照)

X ・ Y のスケーリング

x と y に 1.0 / (1ul << 63) (2^{-63}) を掛けていますが、これは後々 long 型の乱数 (範囲が [-2^{63}, 2^{63}) になります) を直接掛けて [-1, 1) の範囲にすることを想定しているためです。

double 型の仕様上、オーバーフロー・アンダーフローしない限り 2 冪の掛け算で精度が落ちることはありません。

Walker's Alias method のテーブルをまとめる

本来 Walker's Alias method のテーブルは「1 つめの要素の重み」「2 つめの要素のインデックス」の 2 つが必要ですが、これをまとめてしまおうという試みです。

重み firstWeights は正規化してあるので [0, 1) の範囲になっているのですが、これは double 型なのでだいたい 53 bit 程度の精度があります。これを ulong 型 (64 bit) に変換するのですが、 11 bit ほど余ることになります。
ここで、インデックス secondIndexes は [0, 2 ^ 8) なので 8 bit あれば足りますので、一緒の変数に入れてしまおう、という発想です。
メモリアクセスを減らすことができるので、多少は高速化が見込める……かもしれません。

分布に従う乱数の生成

ようやくテーブル生成が終わりました。さて、実際に乱数を生成するコードの説明に移っていきましょう。

// CreateModifiedZigguratTable で生成した定数テーブル  
private static readonly double[] ModifiedZigguratNormalX = { ... };  
private static readonly double[] ModifiedZigguratNormalY = { ... };  
private static readonly ulong[] ModifiedZigguratNormalAliasBox = { ... };  
  
[MethodImpl(MethodImplOptions.AggressiveInlining)]  
public static double ModifiedZigguratNormal<TRng>(TRng rng)  
    where TRng : notnull, RandomBase  
{  
    const int TableSize = 256;  
    // 四角形のレイヤー数  
    const int IMax = 253;  
  
    long u1 = (long)rng.Next();  
    int tableX = (int)(u1 & (TableSize - 1));  
  
    // 四角形のレイヤーなら x 座標を返す  
    if (tableX < IMax)  
    {  
        return u1 * ModifiedZigguratNormalX[tableX];  
    }  
  
    // 以降の処理は相対的に重いため別関数に分け、上の高速パスのインライン化を試みる  
    [MethodImpl(MethodImplOptions.NoInlining)]  
    static double Fallback(TRng rng, long u1)  
    {  
        // CreateModifiedZigguratTable で生成した定数  
        const int InflectionIndex = 204;  
        const ulong MaxConvexRate = 0x3efb83be6450cc00;  
        const ulong MaxConcaveRate = 0x151b6b6b7cd81f00;  
  
        [MethodImpl(MethodImplOptions.AggressiveInlining)]  
        static double SampleX(double x, int tableY) => Math.FusedMultiplyAdd(x, ModifiedZigguratNormalX[tableY - 1] - ModifiedZigguratNormalX[tableY], ModifiedZigguratNormalX[tableY] * (1ul << 63));  
        [MethodImpl(MethodImplOptions.AggressiveInlining)]  
        static double SampleY(double y, int tableY) => Math.FusedMultiplyAdd(y, ModifiedZigguratNormalY[tableY - 1] - ModifiedZigguratNormalY[tableY], ModifiedZigguratNormalY[tableY] * (1ul << 63));  
  
        // Walker's Alias method のテーブルを引く  
        ulong u2 = rng.Next();  
        int tableAlias = (int)(u2 & (TableSize - 1));  
        int tableY = (u2 >> 8) < (ModifiedZigguratNormalAliasBox[tableAlias] >> 8) ? tableAlias : (int)(ModifiedZigguratNormalAliasBox[tableAlias] & (TableSize - 1));  
  
        if (tableY == 0)  
        {  
            // 最下層レイヤー: 尾から生成する  
            double x0 = ModifiedZigguratNormalX[0] * (1ul << 63);  
            double s, t;  
            do  
            {  
                s = ModifiedZigguratExponential(rng) / x0;  
                t = ModifiedZigguratExponential(rng);  
            } while (s * s > t + t);  
            return (x0 + s) * (u1 < 0 ? -1 : 1);  
        }  
        else if (tableY < InflectionIndex)  
        {  
            // へこみレイヤー  
            ulong ux = (ulong)u1 << 1 >> 1;  
            ulong uy = rng.Next() >> 1;  
  
            double tx;  
  
            for (; ; ux = rng.Next() >> 1, uy = rng.Next() >> 1)  
            {  
                // 三角形の右上; 上下左右反転させる  
                if (uy < ux)  
                {  
                    ux = (1ul << 63) - 1 - ux;  
                    uy = (1ul << 63) - 1 - uy;  
                }  
  
                // 三角形の左下; 採択  
                if (uy >= ux + MaxConcaveRate)  
                {  
                    tx = SampleX(ux, tableY);  
                    break;  
                }  
  
                // 確率密度関数より下なら採択  
                tx = SampleX(ux, tableY);  
                double ty = SampleY(uy, tableY);  
  
                if (ty <= Math.Exp(-0.5 * tx * tx))  
                {  
                    break;  
                }  
            }  
            return tx * (u1 < 0 ? -1 : 1);  
        }  
        else if (tableY == InflectionIndex)  
        {  
            // へこみ＋ふくらみレイヤー  
            ulong ux = (ulong)u1 << 1 >> 1;  
            ulong uy = rng.Next() >> 1;  
  
            double tx;  
  
            for (; ; ux = rng.Next() >> 1, uy = rng.Next() >> 1)  
            {  
                // 三角形の左下; 採択  
                if (uy >= ux + MaxConcaveRate)  
                {  
                    tx = SampleX(ux, tableY);  
                    break;  
                }  
  
                // 三角形の右上; 棄却  
                if (uy + MaxConvexRate <= ux)  
                {  
                    continue;  
                }  
  
                // 確率密度関数より下なら採択  
                tx = SampleX(ux, tableY);  
                double ty = SampleY(uy, tableY);  
  
                if (ty <= Math.Exp(-0.5 * tx * tx))  
                {  
                    break;  
                }  
            }  
            return tx * (u1 < 0 ? -1 : 1);  
        }  
        else  
        {  
            // ふくらみレイヤー  
            ulong ux = (ulong)u1 << 1 >> 1;  
            ulong uy = rng.Next() >> 1;  
  
            double tx;  
  
            for (; ; ux = rng.Next() >> 1, uy = rng.Next() >> 1)  
            {  
                // 三角形の左下; 採択  
                if (uy >= ux)  
                {  
                    tx = SampleX(ux, tableY);  
                    break;  
                }  
  
                // 三角形の右上; 棄却  
                if (uy + MaxConvexRate <= ux)  
                {  
                    continue;  
                }  
  
                // 確率密度関数より下なら採択  
                tx = SampleX(ux, tableY);  
                double ty = SampleY(uy, tableY);  
  
                if (ty <= Math.Exp(-tx * tx / 2))  
                {  
                    break;  
                }  
            }  
            return tx * (u1 < 0 ? -1 : 1);  
        }  
    }  
    return Fallback(rng, u1);  
}

大体の工夫は既に述べたとおりですが、一点あるとすればインライン化周りです。

インライン化されたメソッドは、メソッド内部のコードが呼び出し側に埋め込まれます。メソッド呼び出しのオーバーヘッドを省略できるため高速化につながります。 (++C++ を参照 。)
そのため MethodImplAttribute の AggressiveInlining で積極的にインライン化してほしい指定を行っています。

一方、 Fallback() ではわざわざそれを阻害する NoInline を指定しています。これは珍しいかもしれませんが、一応意図があります。
というのも、前述したように全体の約 98 % は Fallback() に到達する前に return します。
そして、 Fallback() には相対的に重く大きいコード (ループなど) が含まれています。したがって、 Fallback() のコードが展開された結果 ModifiedZigguratNormal() 本体のインライン化を阻害する結果にならないよう、あえてメソッド呼び出しとすること (NoInline) を指定しているというわけです。

パフォーマンス

ここまでに挙げた手法のパフォーマンスを比較してみましょう。
BenchmarkDotNet を使って計測しました。

ついでに、正規分布の改良 Ziggurat 法については「AliasBox を Weight と Index の 2 変数に分離した Separate」「ふくらみ・へこみの処理を省略してコードサイズを削った Simple」「tableSize = 128 の 128」についても試して、各手法の有効性を検証してみました。

BenchmarkDotNet=v0.13.5, OS=Windows 11 (10.0.22621.1555/22H2/2022Update/SunValley2)  
12th Gen Intel Core i7-12700F, 1 CPU, 20 logical and 12 physical cores  
.NET SDK=7.0.202  
  [Host]     : .NET 7.0.4 (7.0.423.11508), X64 RyuJIT AVX2  
  DefaultJob : .NET 7.0.4 (7.0.423.11508), X64 RyuJIT AVX2
Method Mean Error StdDev Ratio
Inverse 6.7082 ns 0.1553 ns 0.3690 ns 1.00
ZigguratExponential 4.2090 ns 0.1120 ns 0.2157 ns 0.62
ModifiedZigguratExponential 5.5464 ns 0.1279 ns 0.1570 ns 0.79
BoxMuller 15.3776 ns 0.2602 ns 0.2307 ns 1.00
PolarMethod 13.0116 ns 0.2855 ns 0.3288 ns 0.85
ZigguratNormal 3.3800 ns 0.0815 ns 0.0762 ns 0.22
ModifiedZigguratNormal 0.9127 ns 0.0467 ns 0.0923 ns 0.06
ModifiedZigguratNormalSeparate 1.0547 ns 0.0484 ns 0.0967 ns 0.07
ModifiedZigguratNormalSimple 0.9783 ns 0.0473 ns 0.0750 ns 0.06
ModifiedZigguratNormal128 1.4022 ns 0.0557 ns 0.0704 ns 0.09

なお、 BoxMuller と Polar は一度に 2 個生成するので、実効の時間はこの半分として考えてください。

指数分布では、元々逆関数法もシンプルなためか速度の差は大きくありませんが、それでも改善しています。
また、なぜか改良前の Ziggurat 法のほうが速くなっています。原因については…コードサイズでしょうか…?

正規分布では、 Ziggurat 法が Box-Muller 法・ Polar 法に大きな差をつけており、改良 Ziggurat 法に至っては 1 ns を切っています。
また、 AliasBox で 1 変数にまとめたこと・ふくらみとへこみの処理をきちんと行うことによって、わずかではあるものの加速できていることも分かりました。
また、 tableSize を 128 にした場合 1.5 倍ほどかかるようになってしまいましたが、それでも Polar 法の 5 倍近く高速です。定数テーブルの削減を図りたい場合は採用の余地がありそうです。

おわりに

とても長くなってしまいましたが、 Ziggurat 法と改良 Ziggurat 法について解説しました。
あまり日本語の文献がないので難儀しましたが、この記事をまとめていくうえで私自身の理解も深めることができました。参考になれば幸いです。
もしわかりにくい点・怪しい点などあればご指摘ください。

Ziggurat 法は実装が相対的に複雑なため、ぱっと書けるようなものではないですが、定数テーブルさえ埋め込んでしまえばあとは比較的楽なので、活用できると良さそうです。

最後に、以上に示したコード群をまとめて置いておきます。ご活用ください。
本文では記載しなかった指数分布のコードも含んでいます。

Ziggurat / Modified Ziggurat method

*1:Marsaglia, G., & Tsang, W. W. (2000). The ziggurat method for generating random variables. Journal of statistical software, 5, 1-7.

*2:四辻哲章. (2010). 計算機シミュレーションのための確率分布乱数生成法. プレアデス出版.

*3:McFarland, C. D. (2016). A modified ziggurat algorithm for generating exponentially and normally distributed pseudorandom numbers. Journal of statistical computation and simulation, 86(7), 1281-1294.

*4:Walker, A. J. (1977). An efficient method for generating discrete random variables with general distributions. ACM Transactions on Mathematical Software (TOMS), 3(3), 253-256.